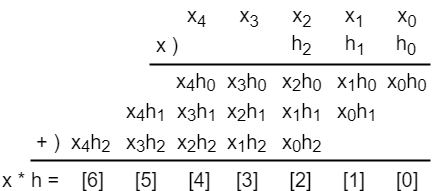第五節 - FFT 的應用二（小規模的線性摺積＆快速多項式乘法）

觀察一下土法煉鋼版本的摺積公式，你會發現 (兩訊號長度皆為$N$的情況下) 其時間複雜度是$\mathcal{O}(N^2)$，而基本上能間接透過傅立葉轉換去計算時域摺積，最根本的原因就是它對應到頻域有著乘積的特性，如果我們現在借助一點 FFT 循環摺積的力量，動些手腳 (科技人常說的 trick) 讓它也能計算線性摺積，那是不是也能把這個操作 (摺積) 的時間複雜度降到$\mathcal O(N\log N)$呢？

# 演算法解說

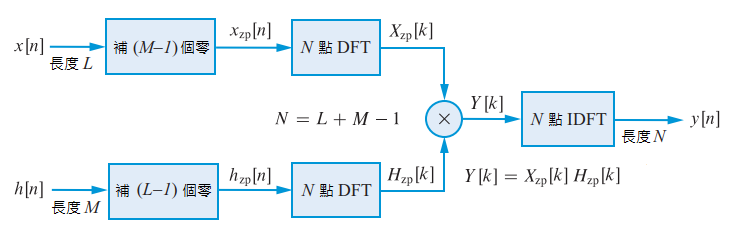
循環摺積顧名思義，就是當一個訊號長度不足以和另一個訊號長度匹配時，便會抓其他時點的值來填充。那我們仔細觀察一下，只要將訊號補零，確保 DFT 抓其他時點的值來填充時一定只會抓到$0$這個值，計算出來的結果便會與單純的線性摺積無異。

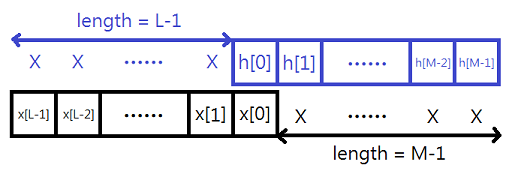
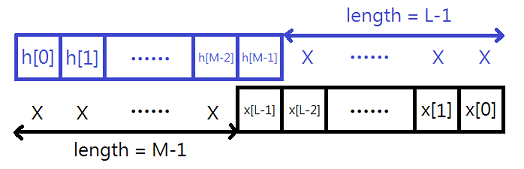
至於補零的長度應該至少要多長？答案是對方的訊號長度少一，原因如下圖，計算第一個時點的摺積時只有自己訊號的第一個時點有和對方訊號匹配，其他時點都會被自己訊號的循環補齊，所以這些部分必須被$0$取代掉；計算最後一個時點的摺積時只有自己訊號的最後一個時點有和對方訊號匹配，其他時點都會被對方訊號的循環補齊，所以這些部分必須被$0$取代掉。

示意圖

演算法架構

MATLAB 呈現

function convWithFFT(u,v)
    l = length(u) + length(v) - 1;
    u = [u, zeros(1,l-length(u))];
    v = [v, zeros(1,l-length(v))];
    return ifft(fft(u).*fft(v)) % 注意在 pointwise operation 情況下是 .* 而不是 *
end

計算實例

• 純數學運算 $\displaystyle \{x_n\} = 1,2,3,4,5$ $\displaystyle \{y_n\} = 10,20,30$ $\displaystyle \{x_n*y_n\}\ = 10,40,100,160,220,220,150$

• 程式碼驗證

    x = [1,2,3,4,5];
    y = [10,20,30];
    convWithFFT(x,y)
    % ans = 10.0000 40.0000 100.0000 160.0000 220.0000 220.0000 150.0000

# 快速多項式乘法 / 大數乘法

快速計算線性摺積還有什麼其他的運用呢？它其實也可以被拿來計算「快速多項式乘法」！

上圖說明一個三次多項式 $x$(降冪排序) 和一個二次多項式 $h$(降冪排序) 相乘的過程 (下標/索引值即為訊號的時間點)，你仔細觀察一下它的算法，這不就是貨真價實的線性摺積 $x[n] * h[n]$ 嗎？只是要注意摺積的結果剛好是升冪排序。正是因為線性摺積和多項式乘法無異，所有能快速計算出線性摺積的方法都能直接應用到多項式乘法。 這邊僅給出一個計算實例作為驗證： 以 $(1-4x+2x^2)(5+7x-x^5) = 5 - 13 x - 18 x^2 + 14 x^3 - x^5 + 4 x^6 - 2 x^7$為例 [6]。

a = [1,-4,2,0,0,0,0,0] % 補齊 1 - 4x + 2x^2 的多項式係數到 8 個點
b = [5,7,0,0,0,-1,0,0] % 補齊 5 + 7x - 1x^5 的多項式係數到 8 個點
ifft(fft(a).*fft(b)) % 兩者的係數再作線性摺積即可
% ans = 5 -13 -18 14 0 -1 4 -2

而數字的乘法也不過就是把每個位數的數字視為係數、基底代入 10 之後再針對結果超過 9 的位數作進位而已，自然可以按照相同的套路去計算它。