第六節 - 各種環境之綜合比較＆淺談積分近似

本節已經到了各種不同環境之傅立葉分析的尾聲 (包含 CTFS、CTFT、DTFT、DTFS)，我們終須將這些式子排在一起比較比較，再觀察一下如果在計算機裡面用黎曼和去逼近積分式，是不是本質上就是自動切換到另外一種環境的分析了呢？

# 綜合比較表

	FS	FT
CT	$\displaystyle \ddot x(t) = \sum_{k=-\infty}^\infty X_{k(f_0)}\ e^{j2\pi(kf_0)t}$ $\displaystyle X_{k(f_0)} = \frac{1}{T_0} \int_{T_0} \ddot x(t)\ e^{-j2\pi(kf_0)t}\ dt$	$\displaystyle x(t) = \int_{-\infty}^{\infty} X(f)\ e^{j2\pi ft}\ df$ $\displaystyle X(f)=\int_{-\infty}^\infty x(t)\ e^{-j2\pi ft}\ dt$
DT 已 歸 一 化	$\displaystyle \ddot x[n] = \sum_{k=<N>} \ddot X_{k(\frac{1}{N})}\ e^{j2\pi(\frac{k}{N})n}$ $\displaystyle \ddot X_{k(\frac{1}{N})} = \frac1N\sum_{n=<N>} \ddot x[n]\ e^{-j2\pi(\frac{k}{N})n}$	$\displaystyle x[n] = \int_1\ddot X(F)\ e^{j2\pi Fn}\ dF$ $\displaystyle \ddot X(F) = \sum_{n=-\infty}^\infty x[n]\ e^{-j2\pi Fn}$

DT	(假) DTFS	DTFT
未 歸 一 化	$\displaystyle \ddot x(nT_s) = f_0\sum_{k=<N>} \ddot X_{k(f_0)}\ e^{j2\pi(kf_0)(nT_s)}$ $\displaystyle \ddot X_{k(f_0)} = T_s\sum_{n=<N>} \ddot x(nT_s)\ e^{-j2\pi(kf_0)(nT_s)}$	$\displaystyle x(nT_s) = \int_{f_s}\ddot X(f)\ e^{j2\pi f(nT_s)}\ df$ $\displaystyle \ddot X(f) = T_s\sum_{n=-\infty}^\infty x(nT_s)\ e^{-j2\pi f(nT_s)}$

* 注意到 (真) DTFS 的 $1/N$是放在分析端，而 (假) DTFS 才是放在合成端。

# 談積分近似這件事

觀察一下黎曼和的定義，你會發現它根本跟取樣無異 (除了取樣間隔造成的倍率縮放)，就如第三章第二節的範例，計算機實作 CTFT 時其實是在做 (未歸一化的) DTFT，而從頻譜返回訊號時理論上是要做 ICTFT，但是頻譜取樣之後就變 ICTFS 了。筆者並不確定積分近似和各種環境有沒有其他更直接的關聯，不過至少到這裡已經把除了 CTFT 以外的環境都和積分近似拉上關係，至少得知它們在其中一個方面的應用了。

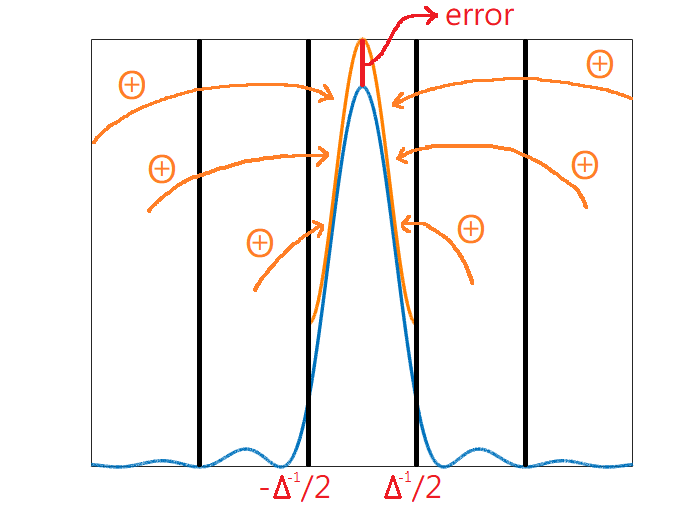
訊號取樣造成頻譜疊加、頻譜取樣造成訊號疊加是我們分別從本章第三、第五節所得知的鐵律，所以根本可以說因為黎曼和間距$\Delta$取得不夠小而在對應域 (時轉頻或頻轉時) 所造成的誤差項即是其他所有和自己差距為間距倒數$\Delta^{-1}$之正整數倍的成分總和，只要對應域不產生混疊效應 (或該效應極不顯著) 那麼誤差項即為純粹的零 (或小到可以忽略)，而且對應域只在$[-\Delta^{-1}/2,\Delta^{-1}/2]$區間內有實質意義。只要把握住這個原則，不隨便就讓取樣產生混疊效應，並注意對應域有效範圍，那我們就確實掌握住「積分近似」這件事。

誤差示意圖	數學敘述
	時域誤差： $\displaystyle \ddot x(t) - x(t) = \sum_{k=1}^\infty x(t-kT_s) + \sum_{k=1}^\infty x(t+kT_s)$ 頻域誤差： $\displaystyle \ddot X(f) - X(f) = \sum_{k=1}^\infty\hspace{-2pt} X(f-kf_s) + \sum_{k=1}^\infty\hspace{-2pt}X(f+kf_s)$

最後想再次強調關於訊號間隔 $T_s$和頻譜間隔$f_0$的限制條件，$T_s$必須至少小於訊號最高頻率 $f_m$之倒數的一半，而 $f_0$必須至少小於訊號長度的倒數，才能避免混疊效應。