本章總結、習題與參考資料

# 本章總結

本章一開始先簡單解釋傅立葉級數理論的發展背景，是由偏微分方程式的解而來，再正式介紹理論，說明正常的訊號都能分解成不同頻率弦波的加權總和 (weighted sum)，特別注意到第六節最後的小結論，如果這個波是週期性訊號的話弦波頻率一定是訊號基頻的整數倍。大部分的教材在介紹連續時間系統時都主要會分成週期性訊號與非週期性訊號兩種情況介紹分別如何求頻譜，而這本書又各帶一個例子來培養感覺，最後再總結兩者之間的比較並解釋為何週期性訊號不適用於傅立葉轉換。

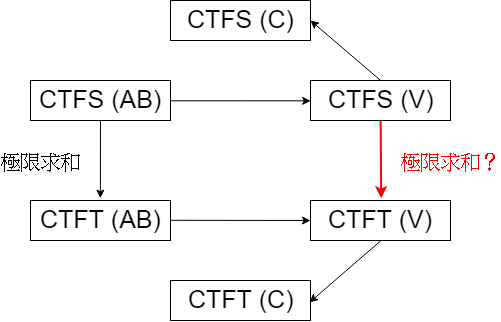
這一章的推導過程冗長但仔細，值得讀者慢慢品味，中間的過渡形式其實不重要，只要記得並且熟練最後 CTFS 和 CTFT 的複數形式 (也就是第六節表格中工程師最常用的 V 版本) 就好，原因我們提過，訊號處理只著重在不同頻率的弦波之間的比例關係，而且 V 版本 (絕對值) 和 C 版本之間有個常數倍的關係，所以說 V版本是比較方便的。到後來你會發現我們仍然都是計算傅立葉轉換居多，因為實務上訊號不可能無限長，當然也就不可能是週期性訊號，因此你可以說傅立葉級數的功能只是提供傅立葉轉換的數學基礎，在現實生活中並不會很常用。

最後再提供一些內文沒講到的補充資料，在歷史方面，PTT 上面有一篇用幽默文筆寫成的優質好文 [28]，而這篇 [29] 是著重在傅立葉轉換的歷史，最後這篇 [30] 感覺很完整但是非免費閱覽，筆者也不知道內容；在數學方面，如果想從線性代數的觀點去解釋那些分解後的弦波可以參考線代啟示錄的這篇 [31]，如果想閱讀濃縮版本的第二、三節可以參考這篇 [32]。

# 延伸習題

  1. 在第二節推導傅立葉係數的過程中有用到「三角函數的正交性」，[20] 提供了兩個方法，方法一是把三角函數化成兩個指數函數的和或差，方法二則是用積化和差公式把兩個三角函數相乘轉為相加減，請讀者選擇其中一個方法把那三條積分式子確實證明出來。如果要選擇第一個方法，必須先證明尤拉公式的乘法與積分：(i) ej(θ1+θ2)=ejθ1ejθ2\displaystyle e^{j(\theta_1+\theta_2)} = e^{j\theta_1}e^{j\theta_2}、(ii)∫θ1θ2ejθdθ=1j[ejθ2−ejθ1]\int_{\theta_1}^{\theta_2} e^{j\theta} d\theta = \frac{1}{j} \big[ e^{j\theta_2} - e^{j\theta_1}\big]。

  3. 在第五節 CTFT 計算範例裡面，最後有個環節是用反轉換驗證原本的計算是對的，這一步有用到一個 恆等式∫−∞∞sin⁡(2πf⋅θ)2πf df=0.5⋅sgn(θ)\int_{-\infty}^{\infty} \frac{\sin(2\pi f\cdot\theta)}{2\pi f}\ df = 0.5\cdot\text{sgn}(\theta)，但是筆者只依靠一組 (θ=1)(\theta=1) [24] 的結果就能知道它會對任意的 θ∈R\theta\in\mathbb R都成立，請問是為什麼呢？

  4. 在第六節的地方有提到，從單邊頻譜稀釋到雙邊頻譜的過程中，量值會因為被正負兩側平分而減半，而主幅角在正頻率部分不變，在負頻率則必須乘上一個負號，文中沒有寫出證明，請說明理由。

  5. 第六節還提到工程師常為了分析方便，會直接減去 (時限) 訊號的平均值，使頻譜直流成分為零。請問為什麼這個動作可以達成他/她想要的效果？除了直流成分之外，其他頻率的成分會不會也跟著改變？

  6. 大部分的訊號與系統課程在討論傅立葉級數對方波 (有尖角的) 的收斂性時都會提到一個很有名的定理叫做「吉布斯現象」(Gibbs phenomenon)，請上網查閱其詳細的定理敘述和相關的動畫或示意圖。

# 參考資料

  1. Baron Fourier, J. B. J. (1878). The analytical theory of heat. The University Press.。《熱的解析理論》之線上英譯版。

  2. Baron Fourier, J. B. J. (1878). The analytical theory of heat. The University Press.。《熱的解析理論》之英譯下載版。

  3. https://www.books.com.tw/products/CN10125415。《熱的解析理論》之中文版目錄。

  4. 蔡志強，〈積分發展的一頁滄桑〉，《數學傳播》二十三卷三期，1999 年 9 月出版。對於傅立葉級數的歷史背景有鉅細靡遺的介紹，也有帶到偏微分方程式。網頁好讀版本：http://episte.math.ntu.edu.tw/articles/mm/mm_23_3_01/page2.html、http://episte.math.ntu.edu.tw/articles/mm/mm_23_3_01/page3.html、http://episte.math.ntu.edu.tw/articles/mm/mm_23_3_01/page4.html。

  5. 林琦焜，〈數學的詩篇 － Fourier 分析〉，《數學傳播》三十五卷三期，2011年 9 月出版。大致講解從弦震動方程到熱傳播問題的背景與偏微分方程解，最後再帶到傅立葉積分。

  6. https://www.math.usm.edu/math/lambers/cos702/cos702_files/docs/Fourier-Series.pdf#page=2 University of Wisconsin–Eau Claire 教授 James S. Walker 所編寫的講義，包含簡單歷史、級數定義，加上各種收斂方式的探討，該寫的都寫在上面了。

  7. Jessop, S. (2017). The Historical Connection of Fourier analysis to Music. The Mathematics Enthusiast, 14(1), 77-100.。也從偏微分的歷史、傅立葉級數，講到傅立葉積分，但是和其他文獻比較起來偏微分的部分著墨較多、較為仔細。

  8. https://www.quora.com/How-did-Fourier-arrive-at-the-Fourier-series。直接從偏微分方程式推導到傅立葉級數的結論。

  9. https://math.stackexchange.com/questions/813031/how-did-fourier-arrive-at-the-following-regarding-his-series-and-coefficients。直接從偏微分方程式推導到傅立葉級數的結論。

  10. Peetre, J. (2000). On Fourier’s discovery of Fourier series and Fourier integrals. preprint.。其中包含了對《熱的解析理論》這本書簡單的導讀。

  11. https://kknews.cc/n/lmeqrxz.html。歐拉、伯努利、達朗貝爾關於弦振動問題的論戰，催生了傅立葉級數。

  12. https://www.youtube.com/watch?v=fT4q4VphjzM&list=PLJlrEjC2PqRdYmXXzWr6mHME6rogX3plK&index=1&t=6m24s。台大電機系連豊力老師的信號與系統課程影片，課程網站可以到http://cc.ee.ntu.edu.tw/~fengli/Teaching/SignalsSystems/ 參考。

  13. https://kknews.cc/news/jmbm4vy.html。這篇偏向傅立葉本人的歷史，極短篇也可以看。

  14. Dirichlet, P. G. L. (2008). Sur la convergence des séries trigonométriques qui servent à représenter une fonction arbitraire entre des limites données. arXiv preprint arXiv:0806.1294.。《關於三角級數的收斂性》之線上英譯版。

  15. Dirichlet, P. G. L. (2008). Sur la convergence des séries trigonométriques qui servent à représenter une fonction arbitraire entre des limites données. arXiv preprint arXiv:0806.1294.。《關於三角級數的收斂性》之英譯下載版。

  16. https://en.wikipedia.org/wiki/Dirichlet_conditions。維基百科的 Dirichlet conditions。

  17. https://cnx.org › exports › dirichlet-conditions-12。非常詳細的 Dirichlet conditions。

  18. http://www.personal.psu.edu/sxt104/class/Math251/Notes-PDE%20pt2.pdf#page=10。裡面有提到看一次微分是否分段連續的收斂條件。

  19. https://www.math24.net/convergence-fourier-series/。簡單提及各種收斂定義與定理。

  20. https://en.wikipedia.org/wiki/Kronecker_delta。維基百科的 Kronecker delta。

  21. https://ocw.mit.edu/courses/mathematics/18-03sc-differential-equations-fall-2011/unit-iii-fourier-series-and-laplace-transform/fourier-series-basics/MIT18_03SCF11_s21_7text.pdf MIT 的課程文件說明如何證明三角函數之間積分的正交性。

  22. https://zh.wikipedia.org/wiki/%E9%BB%8E%E6%9B%BC%E7%A7%AF%E5%88%86。維基百科的黎曼積分。

  23. http://mathworld.wolfram.com/FourierSeriesSquareWave.html。週期性方波的傅立葉轉換。

  24. https://zh.wikipedia.org/wiki/%E7%AA%97%E5%87%BD%E6%95%B0。維基百科的窗函數。

  25. https://www.wolframalpha.com/input/?i=sin%282*pi*f*1%29%2F%282*pi*f%29+df+from+-inf+to+inf 用 WolframAlpha 計算∫−∞∞sin⁡(2πf⋅1)2πf df=0.5\displaystyle \int_{-\infty}^{\infty}\frac{\sin(2\pi f\cdot1)}{2\pi f}\ df = 0.5。

  26. https://zh.wikipedia.org/wiki/%E7%AC%A6%E5%8F%B7%E5%87%BD%E6%95%B0。維基百科的符號函數。

  27. https://zh.wikipedia.org/wiki/Sinc%E5%87%BD%E6%95%B0。維基百科的 sinc 函數。

  28. https://disp.cc/b/163-9eYC。PTT 上鄉民寫的有趣歷史。

  29. https://pulse.embs.org/january-2016/highlights-in-the-history-of-the-fourier-transform/。著重在傅立葉轉換的歷史。

  30. Lokenath Debnath (2012) A short biography of Joseph Fourier and historical development of Fourier series and Fourier transforms, International Journal of Mathematical Education in Science and Technology, 43:5, 589-612, DOI: 10.1080/0020739X.2011.633712。較完整的歷史但是非免費閱覽。

  31. https://ccjou.wordpress.com/2012/03/30/%E5%82%85%E7%AB%8B%E8%91%89%E7%B4%9A%E6%95%B8-%E4%B8%8A/。線代啟示錄，傅立葉級數 (上)。

  32. https://ccjou.wordpress.com/2012/04/03/%E5%82%85%E7%AB%8B%E8%91%89%E7%B4%9A%E6%95%B8-%E4%B8%8B/。線代啟示錄，傅立葉級數 (下)。

Previous第七節 - 週期性訊號之 FT？Next第三章 - 連續時間的訊號處理

Last updated