第五節 - 從 DTFT 取樣到 DTFS

第三節已經示範如何從 CTFT 透過對訊號取樣的方式推導出 DTFT，在本節我們也想依樣畫葫蘆地從 DTFT 透過對頻譜取樣的方式推導出 DTFS，套路和敘述的架構基本上和第三節一模一樣。另外本節前半段會一直宣稱推導出來的結果是「假」DTFS，那只是因為它的頻譜倍率和最終正式的 DTFS 定義稍有不符，所以才分成假/真兩種版本 (其實差不多)。

# (假) DTFS 分析式 (頻譜乃訊號分析)

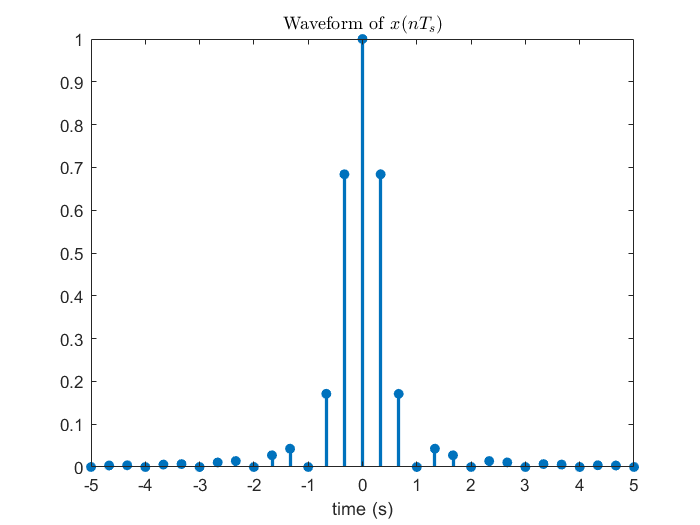
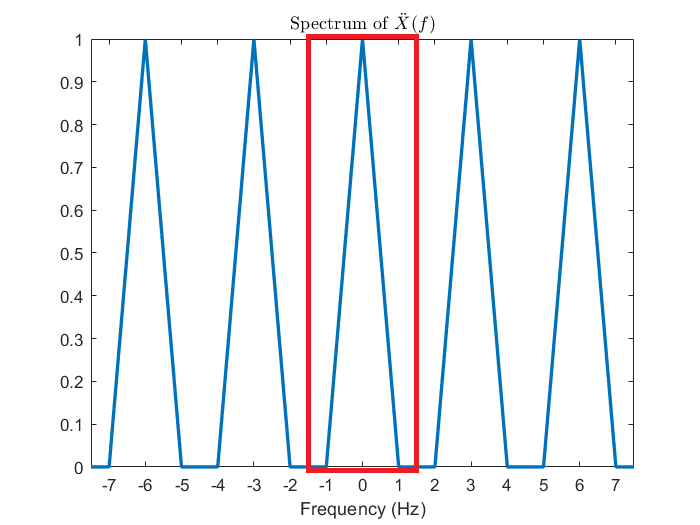
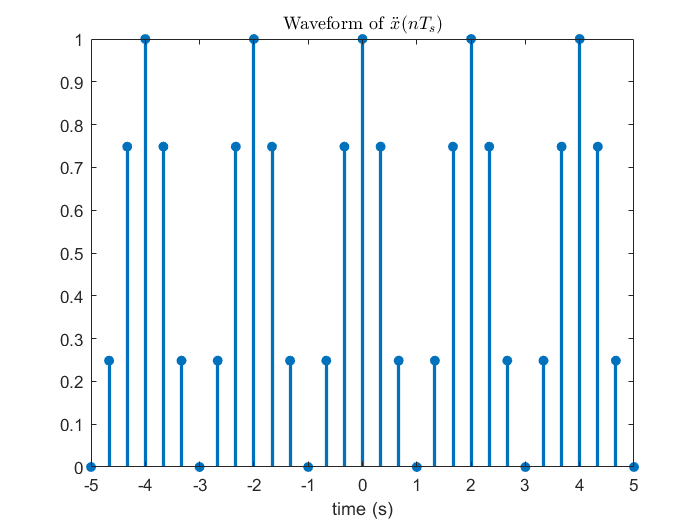
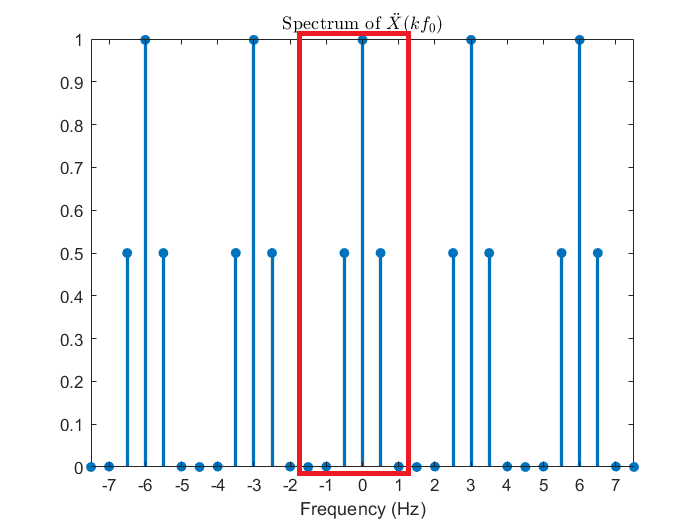
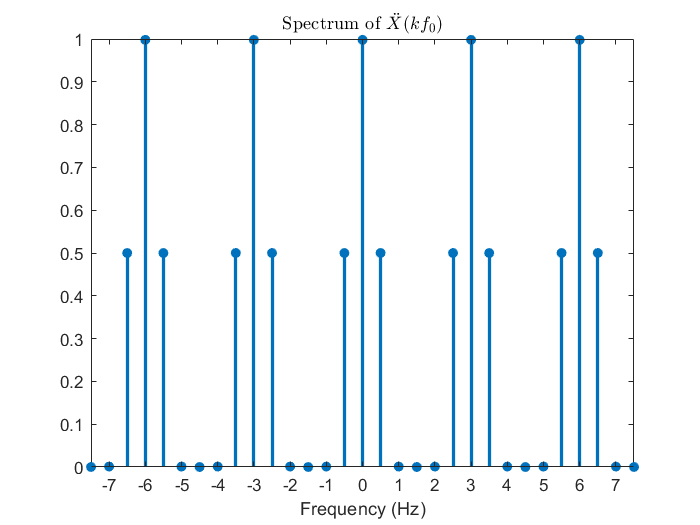
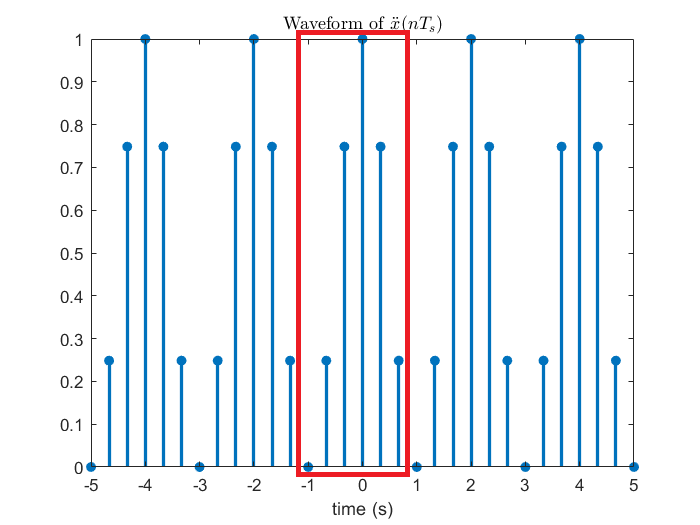
在第三節推導 DTFT 的時候因為是對訊號取樣，所以是從合成端開始分析，由於離散時域視野的限制使得分不出不同頻率的弦波之間的差異；這邊會相反過來，推導 DTFS 時因為是對頻譜取樣，所以得從分析端開始，要想成頻譜是由訊號而來，在弦波頻率是取樣頻率$f_s$切 $N$等分的整數倍的條件下，時間每過$N$個取樣間隔 $T_s$會回到同個函數值，以同樣的語言來說，由於離散頻域視野的限制所以分不出不同時間點之間的差異。先觀賞下面這張沿用第三節範例的示意圖。

	頻域	時域
IDTFT
假 IDTFS	($f_s=3\text{ Hz}$、$f_0=f_s/6=0.5\text{ Hz}$)	($T_s=1/3$s、$T_0=6T_s=2$s)

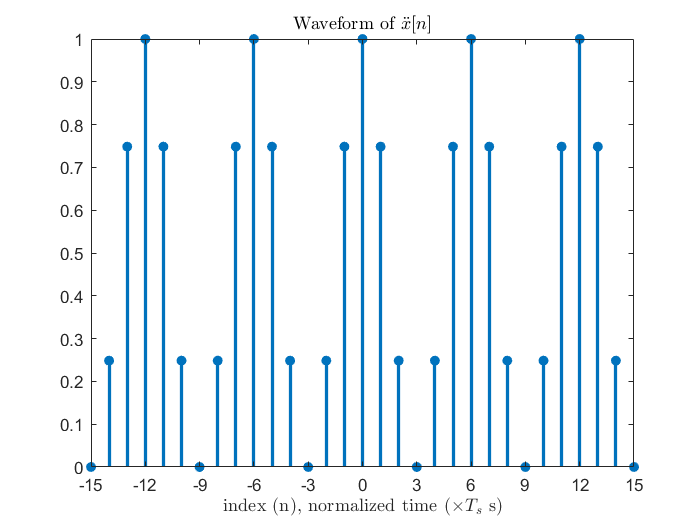
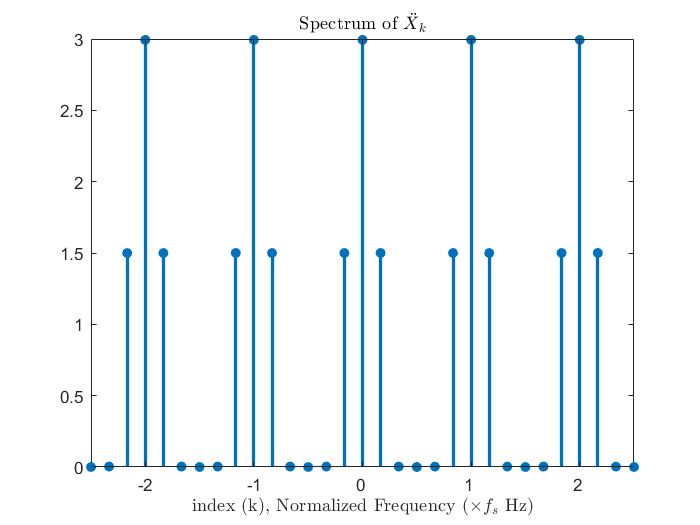
從上圖可以觀察到對連續頻譜 (DTFT) 的一個週期切 $N$等分為離散頻譜 (DTFS) 後，DTFS 的訊號便可以是 DTFT 的訊號以$N$個取樣點為週期平移疊加，讓我們用數學推導再次印證這個結論。(注意到$f_0=f_s/N$這個定義，只要是和 DTFS 相關，包含下一章的 DFT，這個關係式就會存在，不會再重新提醒。)

於是$\displaystyle\ddot x(nT_s) = \sum_{i=-\infty}^\infty x\Big((n+iN)\cdot T_s\Big)$，可以注意到了 DTFS 之後頻譜和訊號都以$N$點為一個週期，週期的點個數是一樣的。而這裡的$f_0$回想一下 CTFS 的定義，其實也就是訊號的基頻阿！

# (假) DTFS 合成式 (訊號由頻譜合成)

分析端的推導告訴我們每一點頻譜都能表示成 $\displaystyle \ddot X(kf_0) = T_s\cdot\sum_{n=<N>}{\ddot x(nT_s)}\cdot e^{-j2\pi(kf_0)(nT_s)}$，現在我們一樣不知道 $\ddot x(nT_s)$到底該怎麼求，還是先來參考一下 DTFT 的解法。

	DTFT	(假) DTFS
分 析 端	$\displaystyle \ddot X(f) = T_s\cdot\sum_{n=-\infty}^\infty x(nT_s)\ e^{-j2\pi f(nT_s)}$	$\displaystyle \ddot X(kf_0) = T_s\cdot\sum_{n=<N>}{\ddot x(nT_s)}\cdot e^{-j2\pi(kf_0)(nT_s)}$
合 成 端	$\displaystyle x(nT_s) = \int_{f_s} \ddot X(f)\ e^{j2\pi f(nT_s)}\ df$	$\displaystyle \ddot x(nT_s) =$？？？

按照第三節的邏輯，最後一格的答案也應該使用$\int$，只可惜現在頻譜也變成離散版本無法使用積分，只好先試試$\sum$可不可行，事後你會發現其實「三角函數的總和 (積分) 也有正交性」，答案至少形如：

　　　　　　　　　　　　　　　　　$\displaystyle \sum_{i=<N>}\ddot X(if_0)\ e^{j2\pi(if_0)(nT_s)}$

此式對$\ddot X(kf_0)$而言包含了想要的項$\ddot X(kf_0)\ e^{j2\pi(kf_0)(nT_s)}$和不想要的項$\displaystyle \sum_{\hspace{-16pt}\substack{i=<N>\\i\not\equiv k\ (\text{mod}\ N)}}\ddot X(if_0)\ e^{j2\pi(if_0)(nT_s)}$

(*) $i\equiv k$，$\displaystyle T_s\sum_{n=<N>}{\hspace{-4pt}\ddot X(kf_0)\ e^{j2\pi(kf_0)(nT_s)}}\cdot e^{-j2\pi(kf_0)(nT_s)} = T_s\sum_{n=<N>}\hspace{-4pt}\ddot X(kf_0) = NT_s\cdot\ddot X(kf_0)$

(*) $i\not\equiv k$，$\displaystyle T_s\sum_{n=<N>}{\ddot X(if_0)\ e^{j2\pi(if_0)(nT_s)}}\cdot e^{-j2\pi(kf_0)(nT_s)}$ 　　　　

所以我們發現了 $\displaystyle T_s\cdot\sum_{n=<N>}{\Bigg(\sum_{i=<N>}\ddot X(if_0)\ e^{j2\pi(if_0)(nT_s)}\Bigg)}\cdot e^{-j2\pi(kf_0)(nT_s)} = NT_s\cdot\ddot X(kf_0)$，和原本的分析端頻譜比起來還多了$NT_s$倍，於是這裡一樣要把它除掉。

　　　　　　　　　　　(未歸一化) 假離散時間傅立葉級數 (fake DTFS)

給定一離散訊號 $x(nT_s)$及其頻譜$\ddot X(f)$，以 $f_0$為取樣間隔會得到離散頻譜$\ddot X(kf_0)$，如果頻譜的取樣間隔恰好平分頻譜的一個週期$\big(f_0 = f_s/N\big)$，那麼：

• 新訊號為舊訊號以 $N$個點 $\big(NT_s = T_0\big)$為週期性疊加，而且能僅從離散頻譜復原回來：

　　　　$\displaystyle \ddot x(nT_s) = \sum_{i=-\infty}^\infty x\Big((n+iN)\cdot T_s\Big) = f_0\cdot\sum_{k=<N>}\ddot X(kf_0)\ e^{j2\pi(kf_0)(nT_s)}$

• 頻譜的取樣點亦可以僅從新訊號的一個週期反推回來：

　　　　　　　　　　$\displaystyle \ddot X(kf_0) = T_s\cdot\sum_{n=<N>}{\ddot x(nT_s)}\cdot e^{-j2\pi(kf_0)(nT_s)}$ 註：上面推導 DTFS 合成端的過程也沒有提到「唯一性」這件事，章末習題會說明如何推導。

# 時間與頻率軸的歸一化

和 DTFT 一樣，按照慣例 DTFS (訊號不變的情況下) 的取樣間隔也必須歸一化成 1，因此取樣頻率 (和頻譜形狀) 會跟著一起歸一化，讀者從上面藍框框的結論一樣可以很快知道歸一化之後的頻譜必須是未歸一化之前的頻率值先壓縮為$1/f_s$倍，振幅再乘以$f_s$倍而來，這其實和 DTFT 結論一樣，不過也很合理，畢竟 FT 和 FS 最根本的差別僅在於訊號有沒有週期性，其他地方其實差異不大。

歸一化	時域	頻域 (注意右下圖 頻率軸 與 振幅 的改變)
前
後

　　　　　　　　　　(已歸一化) 假離散時間傅立葉級數 (fake DTFS)

給定 $N$點一個週期的離散訊號 $\ddot x[n]$，其 $\begin{cases} 分析端：\displaystyle \ddot X_k = \sum_{n=<N>}{\ddot x[n]}\ e^{-j2\pi(\frac kN)n}\\\\合成端：\displaystyle \ddot x[n] = \dfrac1N\cdot\sum_{k=<N>} \ddot X_k\ e^{j2\pi(\frac kN)n}\end{cases}$

註：此歸一化頻譜是由未歸一化頻譜的頻率值先壓縮為$1/f_s$倍，振幅再乘以$f_s$倍而來。

# (真) DTFS

現在終於要來說明什麼是「正式定義」的 DTFS 了，讀者可以發現上面結論的合成端$\ddot X_k$前還出現了$1/N$這個係數，這其實和我們原先對「頻譜」這個詞的印象不符，因為頻譜應該直接要是所對應頻率之弦波的係數，不應該還把殘餘的 $1/N$留在外面，所以說理論上要把這個因子涵蓋進去。

　　　　　　　　　　　　　　離散時間傅立葉級數 (DTFS)

給定 $N$點一個週期的離散訊號 $\ddot x[n]$，其 $\begin{cases} 分析端：\displaystyle \ddot X_k = \dfrac1N\cdot\sum_{n=<N>}{\ddot x[n]}\ e^{-j2\pi(\frac kN)n}\\\\合成端：\displaystyle \ddot x[n] = \sum_{k=<N>} \ddot X_k\ e^{j2\pi(\frac kN)n}\end{cases}$

註：一般訊號與系統課本所介紹的 DTFS 也都是已歸一化的版本。