第三節 - CTFS 的複數形式

上一節我們已經把完整的傅立葉級數都推導完畢！只是讀者如果接觸夠多和訊號系統相關的書籍，會發現工程數學實務上卻都會採用複指數訊號，原因便在於計算的方便 (不用積化和差，光靠指數就能輕鬆把兩個三角函數乘起來)，於是在本節我們必須介紹如何從第二節透過適當的轉換得到複指數訊號。

# 複數形式

　　　　　　　　　　　　　推廣 3 － 複數形式的傅立葉級數

給定一個週期 $T_0$的時域訊號 $\ddot v(t)$，我們必定能將原三角版本的傅立葉級數轉成複數形式：

　　　　　　　　　　　　　　$\displaystyle \ddot v(t) = \sum_{k=-\infty}^\infty V_k\ e^{j2\pi\frac{k}{T_0}t}$

而且對於任何整數 $k$，恆有複係數算法 $\displaystyle V_k = \frac{1}{T_0} \int_{T_0} \ddot v(t)\ e^{-j2\pi\frac{k}{T_0}t} dt$。 註 1：函數上面打兩點代表有週期性的意思，這種表示方式會一直持續到最後，一般的訊號處理課本裡面通常會用 $\widehat v(t)$或 $\widetilde v(t)$表示。 註 2：細心的讀者可能會發現，上一節的係數下標使用 $n$，本節頻譜下標卻使用 $k$，這是因為在後面的章節按照慣例 $n$ 表示時域，$k$ 才表示頻域，所以我們這邊不採用 $V_n$ 而是 $V_k$。

直接從原先的三角函數版本開始吧：

\begin{alignat*}{2}\displaystyle \ddot v(t) &= \dfrac{a_0}2 + \sum_{k=1}^\infty \Big(a_k\cos(k\dfrac{2\pi}{T_0}t) + b_k\sin(k\dfrac{2\pi}{T_0}t)\Big)\\&=\dfrac{a_0}2 + \sum_{k=1}^\infty \Big(a_k\cdot\dfrac{e^{j\theta}+e^{-j\theta}}{2} + b_k\cdot\dfrac{e^{j\theta}-e^{-j\theta}}{2j}\Big)\quad\quad\ //\ 令\ \theta=k\dfrac{2\pi}{T_0}t\\&=\dfrac{a_0}2 + \sum_{k=1}^\infty\Bigg(\Big(\dfrac{a_k}{2}+\dfrac{b_k}{2j}\Big)\ e^{j\theta} + \Big(\dfrac{a_k}{2}-\dfrac{b_k}{2j}\Big)\ e^{-j\theta}\Bigg)\\&=\dfrac{a_0}2 + \sum_{k=1}^\infty\Bigg(\dfrac{a_k-j\ b_k}{2}\cdot e^{j\theta} + \dfrac{a_k+j\ b_k}{2}\cdot e^{-j\theta}\Bigg)\\&=V_0 + \sum_{k=1}^\infty\Bigg(V_k\cdot e^{j\theta} + V_{-k}\cdot e^{-j\theta}\Bigg)\end{alignat*}

其中當 $k>0$： \begin{alignat*}{2} V_k = \dfrac{a_k-j\ b_k}{2} &= \dfrac{\displaystyle\dfrac2{T_0}\int_{T_0} \ddot v(t)\cos(k\dfrac{2\pi}{T_0}t)\ dt - j\ \dfrac2{T_0}\int_{T_0} \ddot v(t)\sin(k\dfrac{2\pi}{T_0}t)\ dt}{2} \\&= \dfrac1{T_0}\displaystyle\int_{T_0} \ddot v(t)\cdot\Big(\cos(k\dfrac{2\pi}{T_0}t)-j\sin(k\dfrac{2\pi}{T_0}t)\Big)\ dt \\&= \dfrac1{T_0}\displaystyle\int_{T_0} \ddot v(t)\ e^{-j2\pi\frac k{T_0}t}\ dt\end{alignat*}

\begin{alignat*}{2} V_{-k} = \dfrac{a_k+j\ b_k}{2} &= \dfrac{\displaystyle\dfrac2{T_0}\int_{T_0} \ddot v(t)\cos(k\dfrac{2\pi}{T_0}t)\ dt + j\ \dfrac2{T_0}\int_{T_0} \ddot v(t)\sin(k\dfrac{2\pi}{T_0}t)\ dt}{2} \\&= \dfrac1{T_0}\displaystyle\int_{T_0} \ddot v(t)\cdot\Big(\cos(k\dfrac{2\pi}{T_0}t)+j\sin(k\dfrac{2\pi}{T_0}t)\Big)\ dt \\&= \dfrac1{T_0}\displaystyle\int_{T_0} \ddot v(t)\ e^{-j2\pi\frac{(-k)}{T_0}t}\ dt\end{alignat*}

當 $k=0$：

$\displaystyle V_0 = \dfrac1{T_0}\int_{T_0} \ddot v(t)\ e^{-j2\pi\frac{0}{T_0}t}\ dt = \dfrac1{T_0}\int_{T_0} \ddot v(t)\ dt = \dfrac{a_0}2$

所以複係數算法的確必須如上面的定理所述！

# 三角疊合

　　　　　　　　　　　　推廣 4 － 三角疊合形式的傅立葉級數

給定一個週期 $T_0$的時域訊號 $\ddot v(t)$，我們必定能將原複數版本的傅立葉級數再化為三角疊合：

　　　　　　　　　　 $\displaystyle \ddot v(t) = C_0 + \sum_{k=1}^\infty C_k\cos(2\pi\frac k{T_0}t+\phi_k)$

其中$\begin{cases} C_0 = V_0&\text{if}\ k=0\ \\C_k = 2 |V_k|,\ \phi_k = \angle V_k&\text{if}\ k>0.\end{cases}$

這節的證明目的在於 $C$和 $V$的關係：

\displaystyle 　　　　　　　\begin{alignat*}{2}C_k \cos(2\pi \frac{k}{T_0} t + \phi_k) &= C_k \frac{e^{j\big[2\pi\frac{k}{T_0}t+\phi_k\big]} + e^{-j\big[2\pi\frac{k}{T_0}t+\phi_k\big]}}{2}\\&= \Big( \frac{C_k}{2}e^{j\phi_k} \Big) e^{j2\pi\frac{k}{T_0}t} + \Big( \frac{C_k}{2}e^{-j\phi_k} \Big) e^{-j2\pi\frac{k}{T_0}t}\\&= V_k\ e^{j2\pi\frac{k}{T_0}t} + V_{-k}\ e^{j2\pi\frac{(-k)}{T_0}t}\end{alignat*}

# 計算範例

複數形式的 CTFS 介紹得差不多了之後，最後我們要以週期性函數裡面較常見的方波作為範例收尾，我們希望能算出一個週期性方波的頻譜。

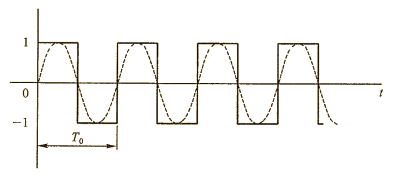
(1) 方波圖形：

(2) 計算係數與驗算：\displaystyle \begin{alignat*}{2} V_k = \frac{1}{T_0} \int_{T_0} \ddot v(t)\ e^{-j2\pi\frac{k}{T_0}t} dt &= \frac{1}{T_0} \Bigg(\int_{-\frac{T_0}{2}}^{0}(-1)\cdot e^{-j2\pi\frac{k}{T_0}t}\ dt + \int_{0}^{\frac{T_0}{2}}1\cdot e^{-j2\pi\frac{k}{T_0}t}\ dt\Bigg) \\&=\frac{1}{T_0} \Bigg( -e^{-j2\pi\frac{k}{T_0}t}\cdot\frac{1}{-j2\pi\frac{k}{T_0}}\bigg|^{0}_{-\frac{T_0}{2}}+e^{-j2\pi\frac{k}{T_0}t}\cdot\frac{1}{-j2\pi\frac{k}{T_0}}\bigg|_{0}^{\frac{T_0}{2}}\Bigg) \\&=\frac{1}{T_0} \Bigg( \frac{e^{-j2\pi\frac{k}{T_0}(-\frac{T_0}{2})}}{-j2\pi\frac{k}{T_0}}+\frac{e^{-j2\pi\frac{k}{T_0}(\frac{T_0}{2})}}{-j2\pi\frac{k}{T_0}}-2\cdot\frac{e^{-j2\pi\frac{k}{T_0}(0)}}{-j2\pi\frac{k}{T_0}}\Bigg)\\&=\frac{1}{-j2\pi k} ( e^{j\pi k} + e^{-j\pi k} -2 )\\&=\frac{ j\ [\cos(\pi k)+\cos(-\pi k)-2] }{2\pi k} = \begin{cases}\displaystyle \frac{-2}{\pi k}j&\text{if }k\text{ is odd}\\0&\text{if }k\text{ is even}\end{cases}\end{alignat*}

\displaystyle \begin{alignat*}{2} \ddot v(t) &=\sum_{\text{odd}\ k} \frac{-2}{\pi k} j\ [\cos(2\pi\dfrac{k}{T_0}t)+j\sin(2\pi\dfrac{k}{T_0}t)] \\&=\Big(j\sum_{\text{odd}\ k} \frac{-2}{\pi k} \cos(2\pi\dfrac{k}{T_0}t)\Big)+\sum_{\text{odd}\ k}\frac{2}{\pi k}\sin(2\pi\dfrac{k}{T_0}t) \\&=\Big(j\cdot0\Big)+\sum_{\text{odd}\ k}\frac{2}{\pi k}\sin(2\pi\dfrac{k}{T_0}t)\\&=\sum_{\text{odd}\ k}\frac{2}{\pi k}\sin(2\pi\dfrac{k}{T_0}t)\\&=\sum_{\text{odd}\ k>0}\frac{4}{\pi k}\sin(2\pi\dfrac{k}{T_0}t) \\&= {4\over\pi}\sin(2\pi\dfrac{1}{T_0}t)+{4\over3\pi}\sin(2\pi\dfrac{3}{T_0}t)+{4\over5\pi}\sin(2\pi\dfrac{5}{T_0}t)+\ ...\end{alignat*} 結果恰好與這篇文 [23] (週期 $2L$) 所給的式子相同，這證明了我們沒算錯！

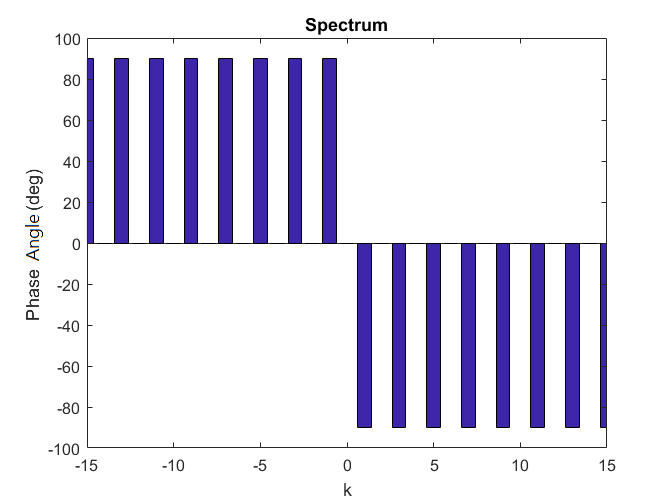
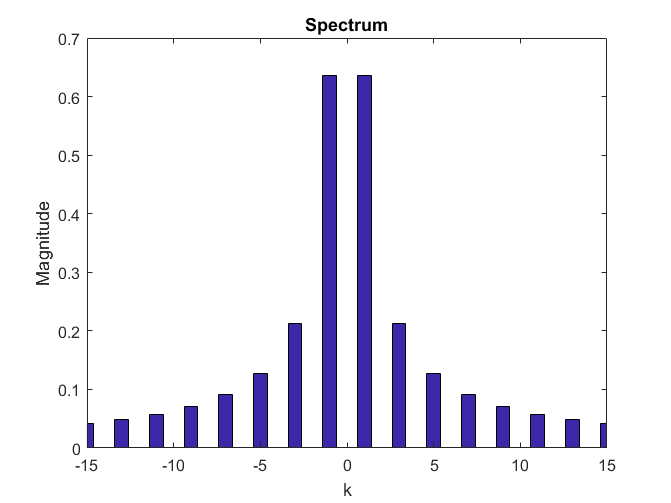
(3) 繪製頻譜以及解讀其物理意義：

量值$|V_k|$	相位角$\angle V_k$

很明顯地，這邊一定是離散頻譜，我們可以觀察到只有在基頻奇數倍的頻率會有值，以基頻波為例，震幅應為 $\displaystyle\frac{2}{\pi}\cdot 2 = \frac{4}{\pi}$，(要乘以 2 是因為正負頻率各占成分的一半)，而相位角也滿足之前的結論，正負頻率會相差一個負號的關係。此例很具體地展現了傅立葉級數理論的實用性。