第五節 - FI 的複數形式 (CTFT)

上一節我們也把傅立葉積分都推導完畢！和 CTFS 一樣，這個東西其實也有複數版本，在本節我們會使用和第三節一模一樣的技巧推導出來。

# 複數形式

　　推廣 2 － 複數形式的傅立葉積分／傅立葉轉換 (CT Fourier Transform，簡稱 CTFT)

給定一個非週期函數 $v(t)$，從其傅立葉積分而來的傅立葉轉換應為：

　　　　　　　　　　　　　$\displaystyle v(t)= \int_{-\infty}^\infty V(f)\ e^{j2\pi ft} df$​

而且對於任意實數$f$，複係數算法可以是 $\displaystyle V(f) = \int_{-\infty}^{\infty} v(t)\ e^{-j2\pi ft} dt$。 註：FT 也是很重要的英文縮寫，後面會常常出現。

我們這邊一樣從第四節的三角函數版本 (FI) 開始出發吧！

\begin{alignat*}{2}\displaystyle v(t) &= \int_{0}^\infty A(f)\cos(2\pi ft) + B(f)\sin(2\pi ft)\ df \\&= \int_{0}^\infty A(f)\cdot\dfrac{e^{j\theta}+e^{-j\theta}}{2} + B(f)\cdot\dfrac{e^{j\theta}-e^{-j\theta}}{2j}\ df\quad\quad\ //\ 令\ \theta=2\pi ft \\&= \int_0^\infty\Big(\dfrac{A(f)}{2}+\dfrac{B(f)}{2j}\Big)\ e^{j\theta} + \Big(\dfrac{A(f)}{2}-\dfrac{B(f)}{2j}\Big)\ e^{-j\theta}\ df \\&=\int_0^\infty V(f)\cdot e^{j\theta} + V(-f)\cdot e^{-j\theta}\ df \\&=\int_{-\infty}^\infty V(f)\cdot e^{j2\pi ft}\ df\end{alignat*}

其中當 $f>0$： \begin{alignat*}{2} V(f) = \dfrac{A(f)-j\ B(f)}{2} &= \dfrac{\displaystyle 2\int_{-\infty}^\infty v(t)\cos(2\pi ft)\ dt - j\cdot2\int_{-\infty}^\infty v(t)\sin(2\pi ft)\ dt}{2} \\&= \displaystyle\int_{-\infty}^\infty v(t)\cdot\Big(\cos(2\pi ft)-j\sin(2\pi ft)\Big)\ dt \\&= \displaystyle\int_{-\infty}^\infty v(t)\ e^{-j2\pi ft}\ dt\end{alignat*}

\begin{alignat*}{2} V(-f) = \dfrac{A(f)+j\ B(f)}{2} &= \dfrac{\displaystyle 2\int_{-\infty}^\infty v(t)\cos(2\pi ft)\ dt + j\cdot2\int_{-\infty}^\infty v(t)\sin(2\pi ft)\ dt}{2} \\&= \displaystyle\int_{-\infty}^\infty v(t)\cdot\Big(\cos(2\pi ft)+j\sin(2\pi ft)\Big)\ dt \\&= \displaystyle\int_{-\infty}^\infty v(t)\ e^{j2\pi ft}\ dt\end{alignat*}

所以複係數算法的確必須如上面的定理所述！有讀者可能發現為什麼上面的推導 (包括前一節的定理結論) 完全沒考慮到 $f=0$ 的情況呢？其實是因為單點函數不影響積分值，也就是說只要 $V(0)$這個值是有限的，我們還是能依賴其他頻率去還原 (recover) 訊號。

# 三角疊合

　　　　　　　　　　　　推廣 3 － 三角疊合形式的傅立葉積分

給定一個非週期性時域訊號 $v(t)$，我們必定能將原複數形式的傅立葉積分再化為三角疊合：

　　　　　　　　　　 $\displaystyle v(t) = \int_{0}^\infty C(f)\cos\Big(2\pi ft + \phi(f)\Big)\ df$

其中 $C(f) = 2 |V(f)|,\ \phi(f) = \angle V(f)\text{, for }f>0.$

這邊也很簡單，直接寫出推導：\displaystyle 　　　　\begin{alignat*}{2}C(f) \cos\Big(2\pi ft + \phi(f)\Big) &= C(f) \frac{e^{j\big[2\pi ft+\phi(f)\big]} + e^{-j\big[2\pi ft+\phi(f)\big]}}{2}\\&= \Big(\frac{C(f)}{2}e^{j\phi(f)} \Big) e^{j2\pi ft} + \Big(\frac{C(f)}{2}e^{-j\phi(f)} \Big) e^{-j2\pi ft}\\&= V(f)\ e^{j2\pi ft} + V(-f)\ e^{-j2\pi ft}\end{alignat*}

# 計算範例

最後我們依然要以一個例子作為本節的結束，在實務上處理訊號的時候我們只會從很長的原始檔之中擷取其中一小段，就相當於在時域上乘以一個窗函數 [24]，如果我們好奇這個動作究竟會在頻域產生什麼樣的效果，就得先觀察窗函數在頻譜上的圖形，於是我們想拿這個當作範例。

(1) 訊號圖形：(脈波只是窗函數的其中一種)

(2) 計算頻譜與驗算：(記號 $\mathcal F\{\omega(t)\}(f)$代表 $\omega(t)$這個訊號的傅立葉轉換，是以頻率$f$為輸入的函數)

$\displaystyle \mathcal F\{\omega(t)\}(f) = \int_{-\frac{T_0}2}^{\frac{T_0}2} e^{-j2\pi ft}\ dt = \begin{cases}T_0&\text{ if }f=0 \\\\\dfrac{\sin(\pi f\cdot T_0)}{\pi f\cdot T_0}\cdot T_0&\text{ if }f\ne0\end{cases}$

其中$f\ne0$ 的推導如右：$\dfrac{1}{-j2\pi f} e^{-j2\pi ft}\ \bigg| _{t=-\frac{T_0}2}^{t=\frac{T_0}2} = \dfrac{2\cdot j\sin(-2\pi f\cdot\frac{T_0}2)}{-j2\pi f} = \dfrac{\sin(\pi f\cdot T_0)}{\pi f}$ \displaystyle \begin{alignat*}{2}\omega(t) = \int_{-\infty}^{\infty} \mathcal F\{\omega(t)\}(f)\ e^{j2\pi ft}\ df &= \int_{-\infty}^{\infty} \dfrac{\sin(\pi f\cdot T_0)}{\pi f}\cdot e^{j2\pi ft}\ df\\&= \int_{-\infty}^{\infty} \dfrac{\sin(\pi f\cdot T_0)}{\pi f} \big(\cos(2\pi ft)+j\sin(2\pi ft)\ \big)\ df\quad\quad\ //\ 右邊的 \sin 和括號外面相乘會得到奇函數，積分值為零\\&= \int_{-\infty}^{\infty} \dfrac{\sin(2\pi f\cdot \frac{T_0}2)\cos(2\pi ft)}{\pi f}\ df \\&= \int_{-\infty}^{\infty} \dfrac{\sin\Big(2\pi f\cdot (\frac{T_0}2+t)\Big)+\sin\Big(2\pi f\cdot (\frac{T_0}2-t)\Big)}{2\pi f}\ df\quad\quad\ //\ 積化和差 \\&= \int_{-\infty}^{\infty} \dfrac{\sin\Big(2\pi f\cdot (\frac{T_0}2+t)\Big)}{2\pi f}\ df + \int_{-\infty}^{\infty} \dfrac{\sin\Big(2\pi f\cdot (\frac{T_0}2-t)\Big)}{2\pi f}\ df\end{alignat*} 其中注意這個積分 $\displaystyle\int_{-\infty}^{\infty} \dfrac{\sin\Big(2\pi f\cdot\theta\Big)}{2\pi f}\ df = 0.5\cdot\text{sgn}(\theta)$ [25]，符號函數 $\text{sgn}$ 的定義如 [26] 所述。

於是乎驗算的結果與上面的訊號圖形相吻合，這證明了我們沒算錯！

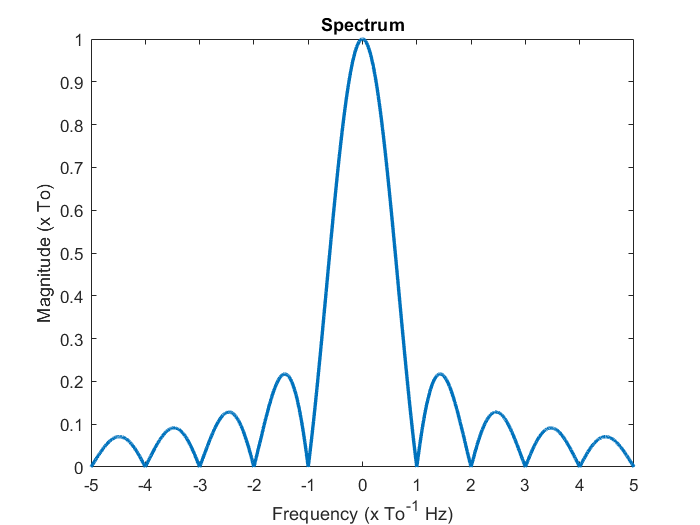
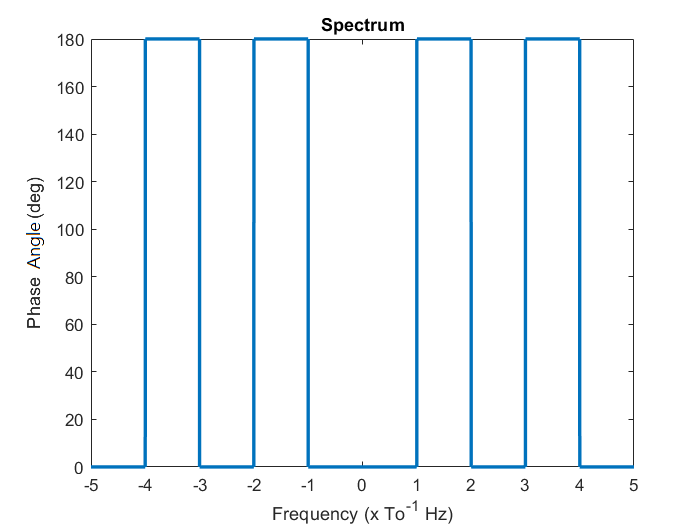
(3) 繪製頻譜以及解讀其物理意義：

量值$|V(f)|$	相位角$\angle V(f)$

很顯然地，這邊必須是連續頻譜，我們可以觀察到在$f=0$ 時有最大值，其餘都跟隨我們推導出來的頻譜函數，隨著頻率增加而成分遞減，而這也符合我們使用的訊號，只在 $t = -\frac{T_0}2$和 $t = \frac{T_0}2$有值的變化，在其餘時點皆是固定常數，自然低頻成分較高。而相位角也滿足我們前一節的推導，正負頻率會相差一個負號 ($-0^\circ=0^\circ$、$-180^\circ = 180^\circ$)。此例子亦具體的展現了傅立葉轉換理論的實用性。

(4) 介紹 sinc 函數：

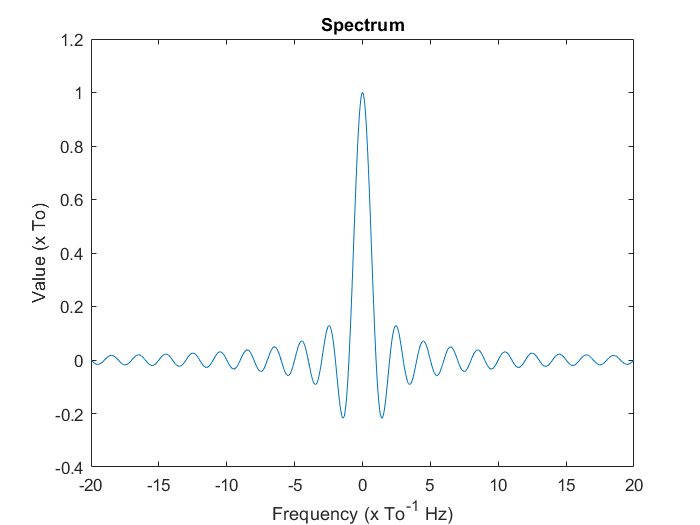
細心的讀者應該會發現，這個例子的相位角不是 0 度就是 180 度，這意味著整段頻譜都是實數，可以直接畫在座標平面上，不需要相位角的輔助，將量值和相位角合併之後的頻譜如下：

如果只看數字刻度 (忽略掉 $T_0$尺度伸縮) 的話，這個圖形就是我們鼎鼎有名的 sinc 函數 [27]，這個函數在訊號處理領域中很常出現，專業人士幾乎沒有人不認識它。