第四節 - FFT 的應用一（離散時間的訊號處理）

前面講了那麼久的 DFT (和 FFT)，這一節終於要來介紹它的第一個應用了！在第四章第六節已經暗示同時對訊號和頻譜作積分近似其實就是 (未歸一化的) DTFS，而它和 DFT 有 87% 像，與其那麼辛苦手刻定積分運算，為什麼不直接使用 DFT 進行離散訊號處理呢？它的好處大概在於，這是一個已標準化的運算流程，而且上一節也已經介紹一個能大幅度降低計算 DFT 時間複雜度的演算法 FFT，有些程式語言例如 MATLAB 就有已包裝好的單行函式 fft，以節省工程師的時間。在本節我們一樣會展示如何用 DFT 對第三章第二節的範例進行濾波，並比較分析結果的異同。

# 比較 DFT 與積分近似

	合成端	分析端
積分 近似	$\displaystyle \ddot x(nT_s) = f_0\sum_{k=<N>} \ddot X_{k(f_0)}\ e^{j2\pi(kf_0)(nT_s)}$	$\displaystyle \ddot X_{k(f_0)} = T_s\sum_{n=<N>} \ddot x(nT_s)\ e^{-j2\pi(kf_0)(nT_s)}$
DFT	$\displaystyle x[n]={1\over N}\sum _{k=0}^{N-1}X[k]\ e^{j2\pi(kf_0)(nT_s)}$	$\displaystyle X[k]=\sum _{n=0}^{N-1}x[n]\ e^{-j2\pi(kf_0)(nT_s)}$

很明顯地，標準 DFT 的頻譜是積分近似的版本還要多乘以一個取樣頻率$f_s$作為縮放倍數。

# 再重複一次之前的實驗

現在讀者應該已經對 DFT 有一定程度的認識了，讓我們把第三章第二節範例的步驟修改如下 (建議可以開新分頁和之前的範例對照著看)： (1) 產生範例弦波 (2) 用 DFT 分析弦波成分 (3) 決定欲留下的頻率成分、並把不需要的成分濾除 (4) 對處理過後的頻譜作 IDFT 獲得還原後的範例弦波！

Step 1. 產生範例弦波

這邊一樣沿用第三章的範例： x(t)=\begin{cases} A_1\sin(2\pi f_1t)+A_2\sin(2\pi f_2t)&\text{ for }0\le t\le 6 \\ 0&\text{ otherwise,} \end{cases}\quad\text{where}\begin{array}\ (f_1,A_1)=(1,10),\\ (f_2,A_2)=(8,2).\color{white}0\end{array}

dt = 0.005; % 時間軸間隔
t_axis = (0:dt:6-dt); % 時間軸，從 0 到 6 秒，每 dt 秒為一間隔，想想看為什麼最後一格是 6-dt 而不是 6
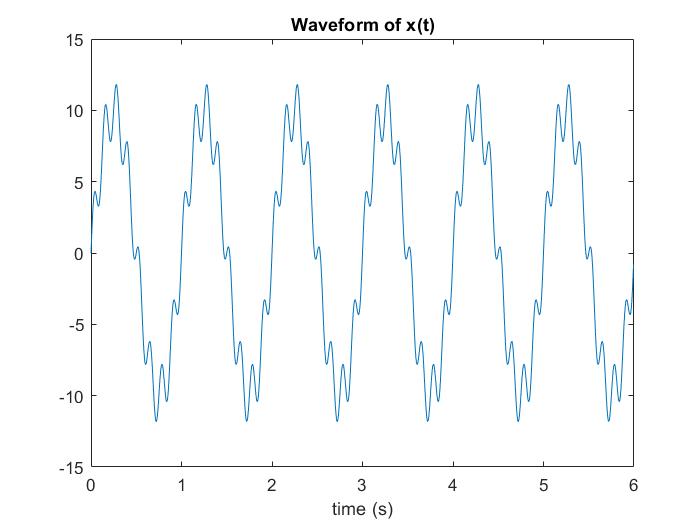
x = 10*sin(2*pi*1*t_axis) + 2*sin(2*pi*8*t_axis); % 波型

% 以下畫圖
figure;
plot(t_axis,x);
xlabel('time (s)');
ylabel('x(t)');
title('Waveform of x(t)');

可觀察到除了有主頻率 1 Hz 的大波外，每一秒內也各有 8 個小波峰與小波谷，代表也隱含 8 Hz 的小波。

Step 2. 用 DFT 分析弦波成分

N = length(x); % DFT 點數
fs = 1/dt; % 原時域訊號的取樣頻率，同時也是 DFT 頻譜一個有效週期的長度
df = fs/N; % 除以點數進而得到頻譜一格所對應到的頻率差距
X = fft(x); % 進行快速離散傅立葉轉換
X = fftshift(X); % 因為 fft 函式顯示的範圍在 [0,fs)，所以要把右半邊移到左半邊，讓頻率為零的成分移到正中央：(-fs/2,fs/2]
f_axis = fftshift((0:df:fs-df)); % 計算頻譜刻度
i=1;
while f_axis(i) ~= 0
    f_axis(i) = f_axis(i) - fs;
    i = i + 1;
end % 並且讓頻率為零的刻度移到正中央

% 因為時域訊號的成分理論上僅會發生在 1Hz、8Hz 的地方，
% 原頻譜有效週期長度 200Hz 卻遠大於我們所需要的，因此
% 這邊顯示的時候僅擷取 -10Hz ~ 10Hz 的部分。
% 讀者可先註解掉此段、顯示全段的版本，再來做調整。
X_show = X(int32(length(X)*0.451):int32(length(X)*0.55));
f_axis_show = f_axis(int32(length(f_axis)*0.451):int32(length(f_axis)*0.55));

% 以下畫圖
figure;
plot(f_axis_show, abs(X_show)/fs); % 為了和第三章的 CTFT 一致，還要除以 fs
yticks((0:6:30));
xlabel('Frequency (Hz)');
ylabel('abs(X(f))');
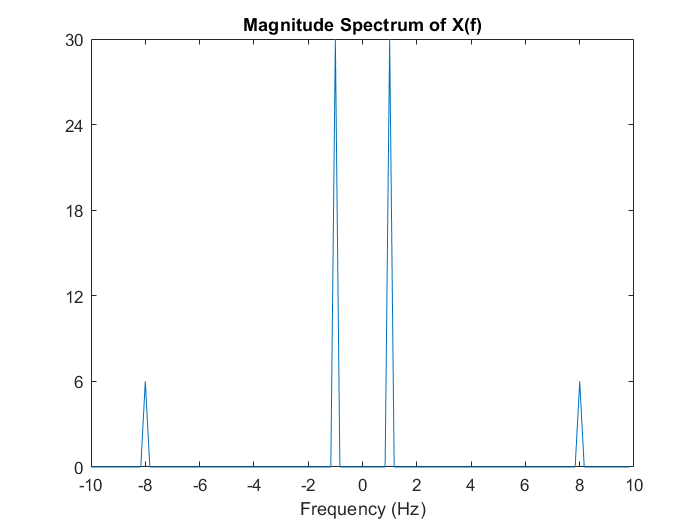
title('Magnitude Spectrum of X(f)');

發現結果和第三章的實驗以及肉眼的觀測相吻合，有 1 Hz 和 8 Hz 兩種成分，且兩者量值相差五倍。

Step 3. 決定欲留下的頻率成分、並把不需要的成分濾除

和第三章採取的策略相同，使用截止頻率為 4 Hz 的低通濾波器，也就是只保留 -4 Hz ~ 4 Hz 的成分。

X(1:int32(length(X)*0.48)) = 0; % 濾除小於 -4 Hz 的成分
X(int32(length(X)*0.52):end) = 0; % 濾除大於 4 Hz 的成分

% 和 Step 2 一樣只顯示 -10Hz ~ 10Hz 的部分。
X_show = X(int32(length(X)*0.451):int32(length(X)*0.55));
f_axis_show = f_axis(int32(length(f_axis)*0.451):int32(length(f_axis)*0.55));

% 以下畫圖
figure;
plot(f_axis_show, abs(X_show)/fs); % 為了和第三章的 CTFT 一致，還要除以 fs。為什麼？
xlabel('Frequency (Hz)');
ylabel('abs(X(f))');
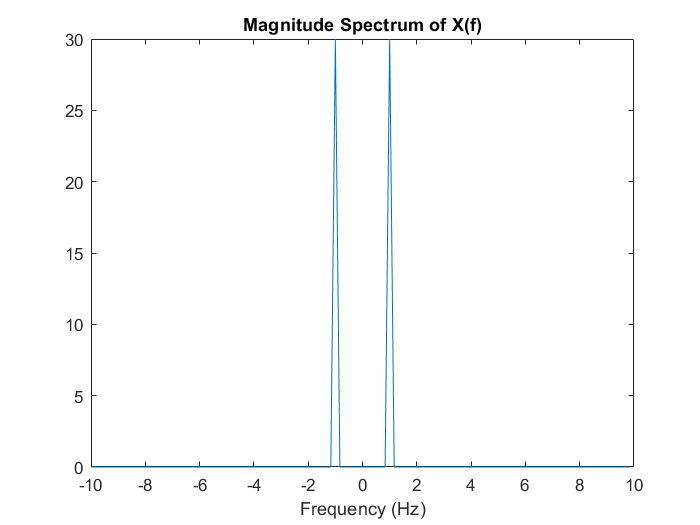
title('Magnitude Spectrum of X(f)');

發現確實有濾掉 8 Hz 的成分！

Step 4. 對處理過後的頻譜作 IDFT 獲得還原後的範例弦波！

y = ifft(ifftshift(X)); % 先讓頻率為零的成分移到最左邊，再作傅立葉反轉換
y = real(y); % 理論上這裡的還原訊號應該只會出現實部，因為計算機浮點數的誤差，
% 偶爾還是會產生少許的虛部訊號，因此必須使用 real 函式把實部取出來。

% 以下畫圖
figure;
plot(t_axis,y);
xlabel('time (s)');
ylabel('y(t)');
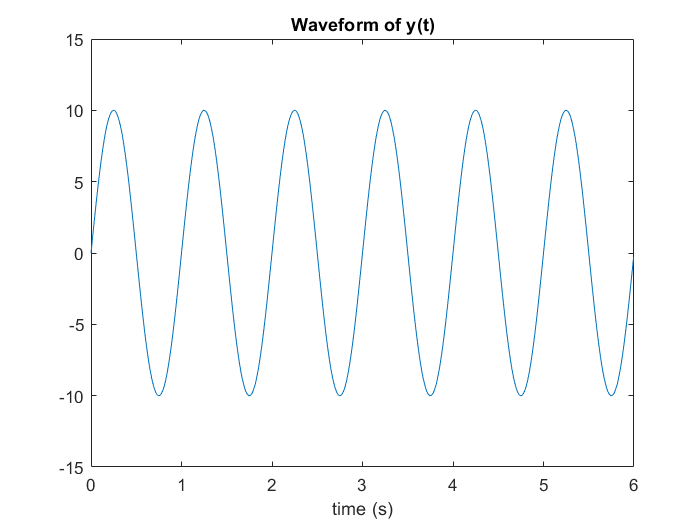
title('Waveform of y(t)');

觀察一下發現 8 Hz 的小波雜訊的確不見了！而且這個波形看起來比第三章的實驗還要整齊，至此我們成功地運用了 DFT 這個強大的工具進行濾波操作！這樣就不用再像第三章一樣手刻 (土法煉鋼) CTFT 程式碼，也能利用 FFT 這個有效率的演算法加速運算了。