第四節 - 取樣定理及訊號還原

上一節已經告訴我們對連續訊號取樣會造成頻譜週期性疊加，如何從疊加後的頻譜還原出原始的連續訊號亦是一大課題，本節將討論在什麼條件之下可以無失真的還原及其操作方式。

# 取樣定理

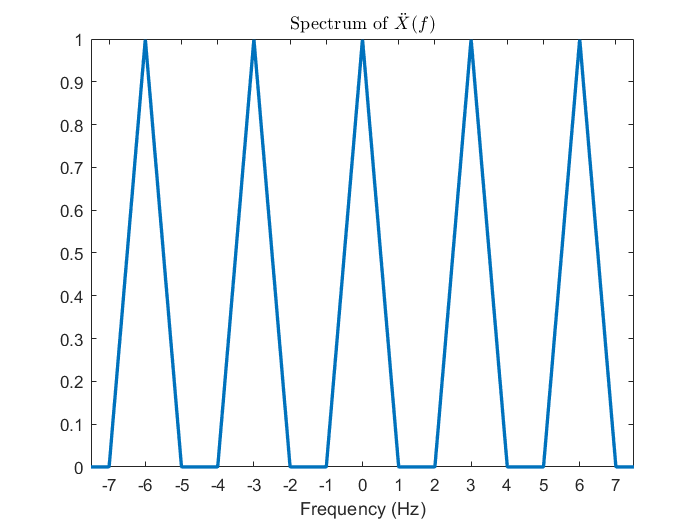
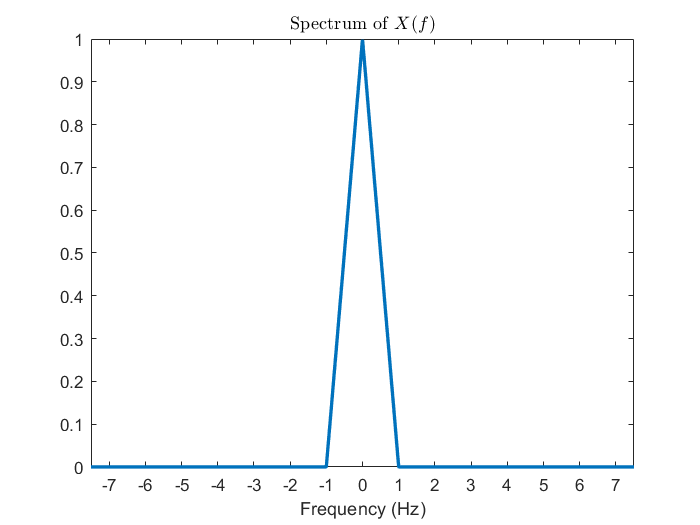
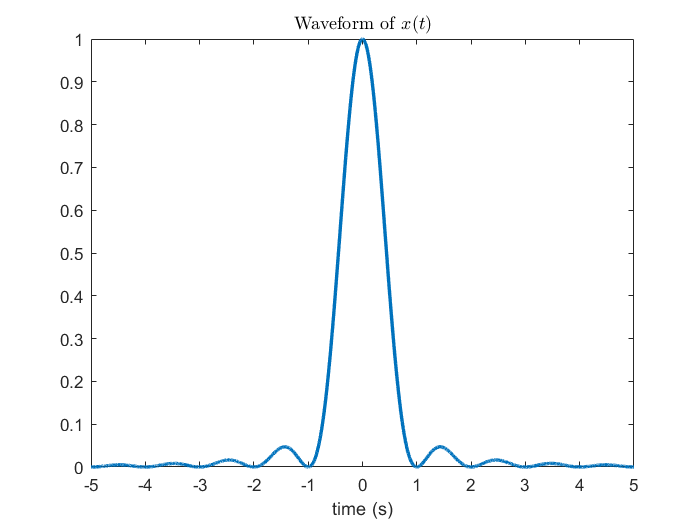
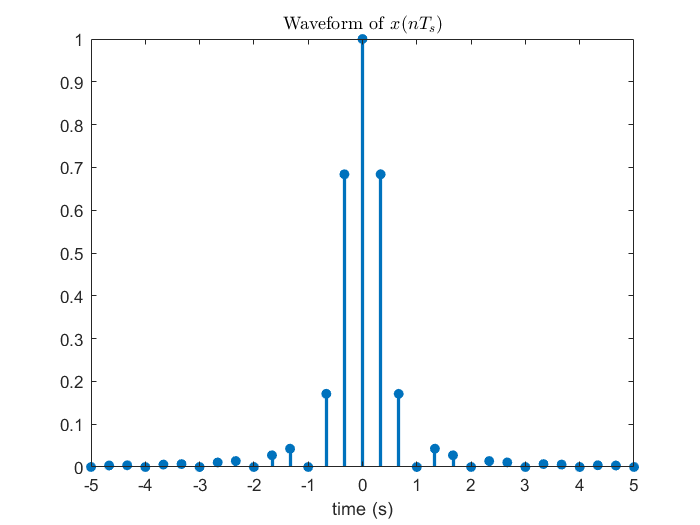
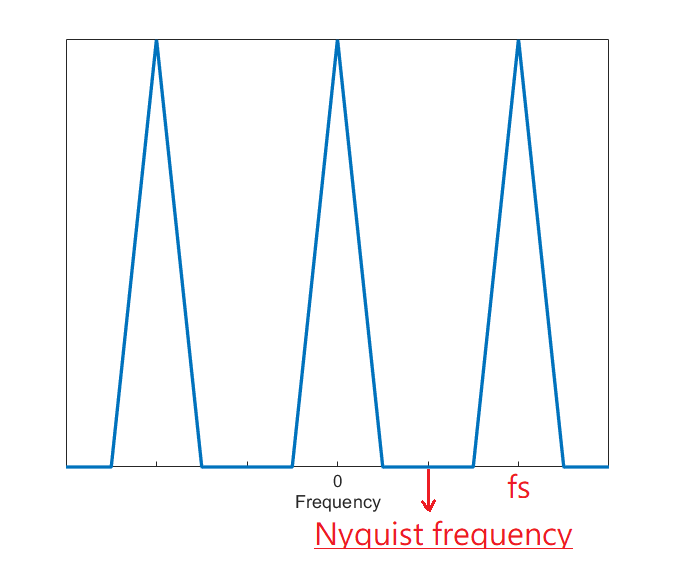
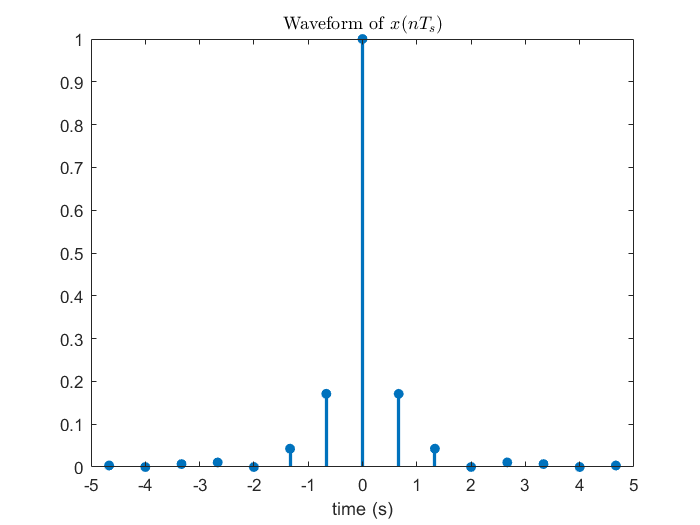
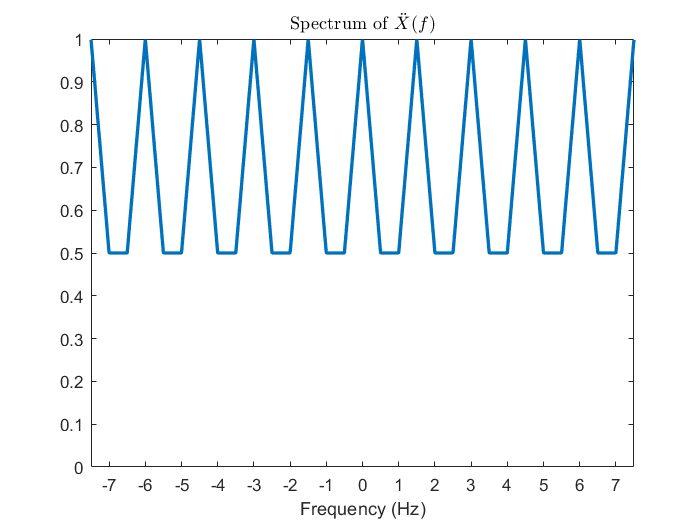
在正式介紹取樣定理之前，我們想先從前一節使用的例子$\mathcal F\{\text{sinc}^2(t)\} = \max\{0,\ 1-|f|\}$開始觀察，這個例子的好處是它的頻率範圍是有限的$[-1,1]$，這樣才能確保在適當的條件下能無失真還原。一開始先繪出 CTFT 組圖，接著 DTFT 告訴我們當連續訊號以每 $T_s$秒取樣一次，頻譜會每$f_s$赫茲疊加一次，於是從 3 Hz 開始漸漸地往下調整，2 Hz、1.5 Hz，到最後的 1 Hz，我們會發現到 2 Hz 之前頻譜都還沒發生混疊 (aliasing) 現象，也就是在$[-1,1]$這個頻率區間的頻譜還沒被汙染到，唯有當$f_s$降到了 2 Hz 以下之後由於不同區間的頻譜彼此之間靠太近才開始互相影響。

	時域	頻域
CTFT $f_s\to\infty$
DTFT (沒有混疊) $f_s=3\text{ Hz}$
DTFT (快要混疊) $f_s=2\text{ Hz}$
DTFT (已經混疊) $f_s=\frac32\text{ Hz}$
DTFT (嚴重混疊) $f_s=1\text{ Hz}$

　　　　　　　　　　取樣定理 (Nyquist-Shannon Sampling Theorem) [5]

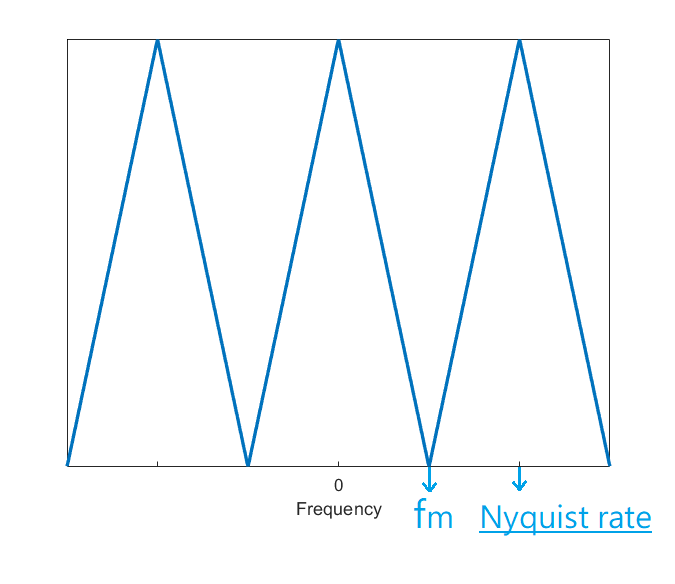
考慮有限頻寬 (band-limited) 訊號 $x(t)$，其最高頻率令為$f_m$，那麼當取樣頻率$f_s > 2f_m$的時候原訊號 $x(t)$可僅由取樣後的 $x[n] = x(nT_s)$進行無失真重建。

• 如果給定$f_m$，那麼可以接受的最低取樣頻率 $2f_m$稱為奈奎斯特速率 (Nyquist rate)。 　　　　　　　　　　　　　 　　　　　　　
• 如果給定$f_s$，那麼要確保取樣後還能完全復原的最高可接受訊號頻率 $f_s/2$ 為奈奎斯特 頻率 (Nyquist frequency)。 　　　　　　　　　　

# 如何重建 CT 訊號

	頻域	時域
IDTFT
ICTFT

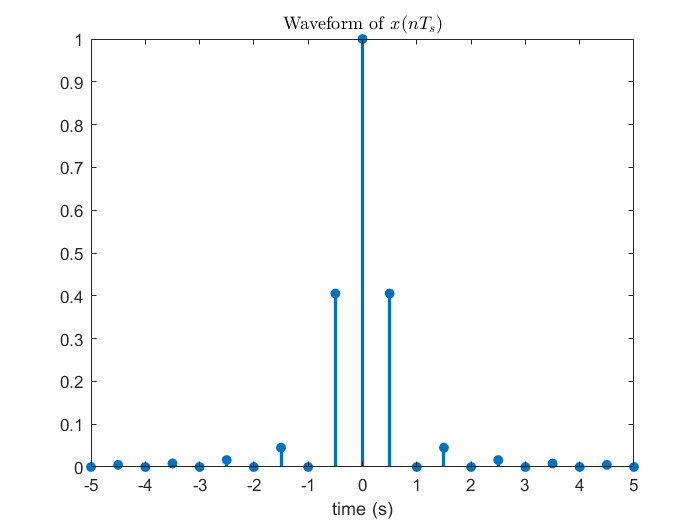
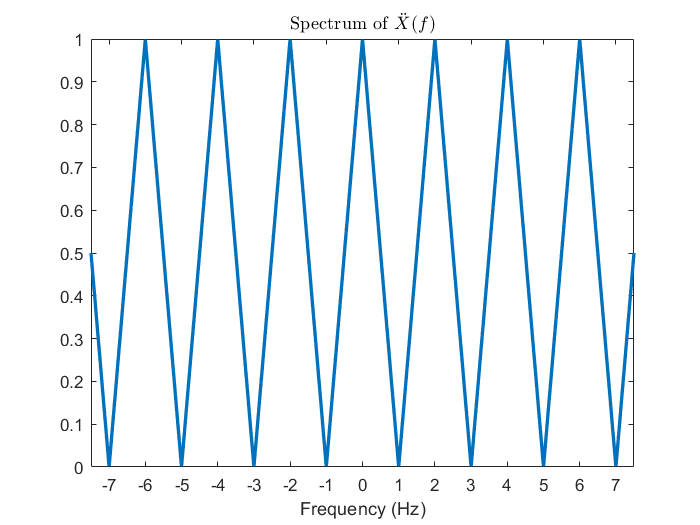
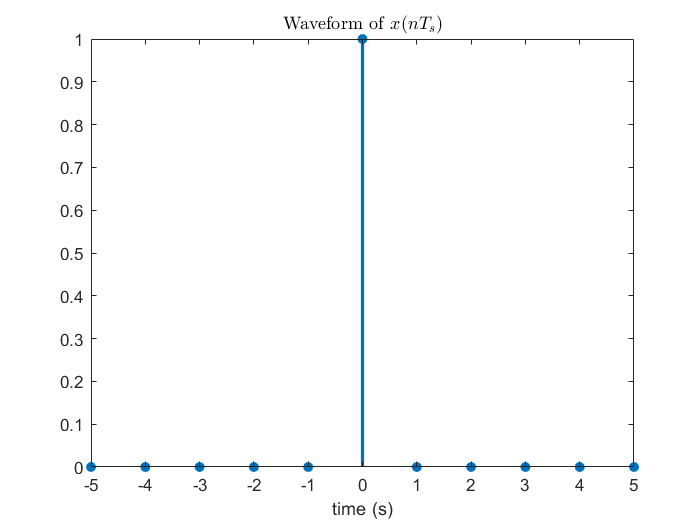
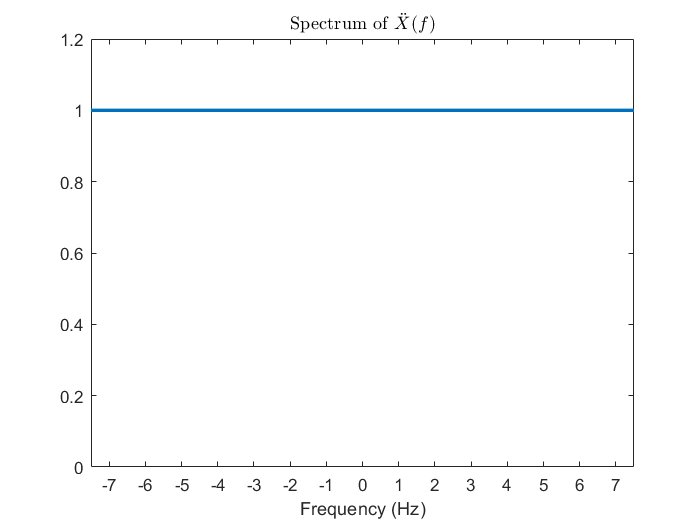
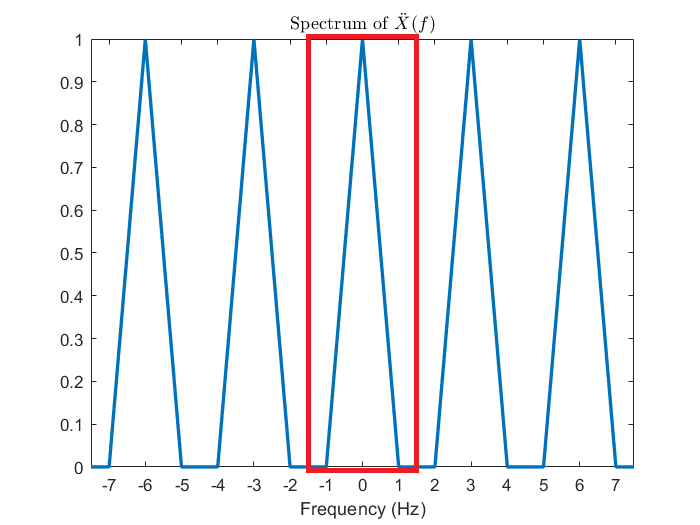
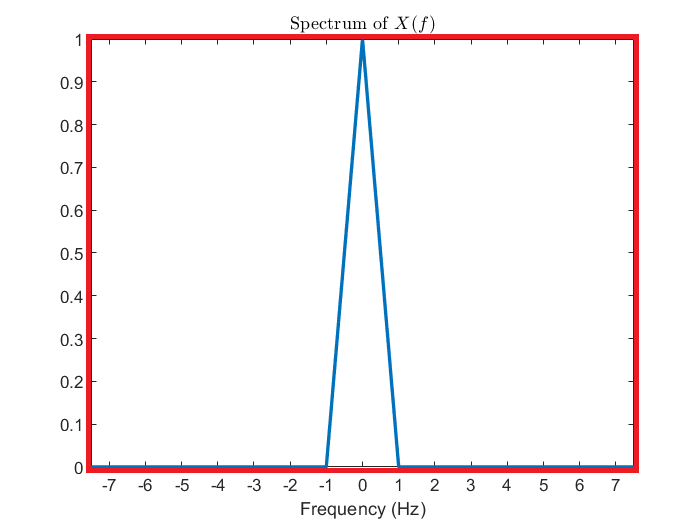
一張圖勝過千言萬語。對 DTFT 來說，因為頻譜只包含一個週期的資訊，所以只能還原出離散訊號；但是對 CTFT 來說，頻譜可是包含了整個實數域的資訊 (比 DTFT 豐富許多)，因此它就能還原出整組連續訊號。我們還能發現到，如果訊號滿足取樣定理的話，其實它的頻譜也可以自動地從 DTFT 延伸到 CTFT。

\displaystyle \begin{alignat*}{2}x(t) &= \int_{-\infty}^{\infty} X(f)\ e^{j2\pi ft}\ df \\&= \int_{-\infty}^{-0.5f_s} X(f)\ e^{j2\pi ft}\ df + \int_{-0.5f_s}^{0.5f_s} X(f)\ e^{j2\pi ft}\ df + \int_{0.5f_s}^{\infty} X(f)\ e^{j2\pi ft}\ df \\&= \int_{-\infty}^{-0.5f_s} 0\cdot e^{j2\pi ft}\ df + \int_{-0.5f_s}^{0.5f_s} X(f)\ e^{j2\pi ft}\ df + \int_{0.5f_s}^{\infty} 0\cdot e^{j2\pi ft}\ df \\&= \int_{-0.5f_s}^{0.5f_s} X(f)\ e^{j2\pi ft}\ df \\&= \int_{-0.5f_s}^{0.5f_s} \ddot X(f)\ e^{j2\pi ft}\ df\end{alignat*}

於是在這個情況之下的連續訊號也能從 DTFT 頻譜還原。