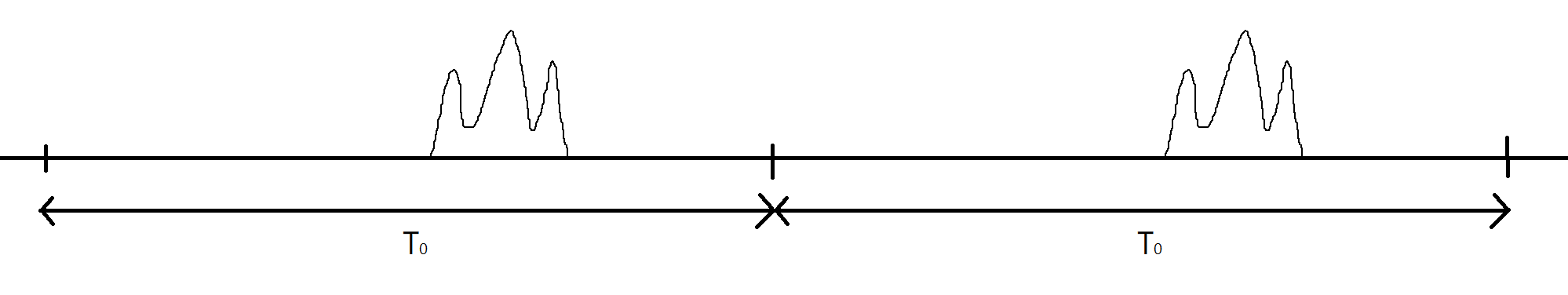第四節 - 傅立葉積分 (FI)

前一節已經簡單介紹過如何分析週期性訊號的頻譜成分了！相信讀者對於頻譜一詞已有一定概念。在現實生活中，我們不可能一次就處理無窮無盡的訊號，勢必要擷取一部份來進行，所以待處理的訊號不可能有週期性。在這一節，我們將要介紹分析非週期性訊號頻譜成分的方法。與第二節雷同，這邊仍然會以嚴謹的數學論證推導出傅立葉積分公式，只不過要借助第二節週期性的數學結果，加上一點技巧方能達成。

# 時限的圖解與證明

對於一個時限 (time-limited) 訊號，我們可否仍將之近似為一個週期性訊號呢？是可以的，其實只不過就是先假設它有週期 $T_0$，再把週期的值慢慢拉遠，遠到我們觀察不到重複性，最後變成無窮遠，那就是我們要的了。概念圖如下：

I. 一開始設定週期不是很大的時候，在同個視窗下很容易看到多個波型。

II. 接下來設定週期愈來愈大的時候，在同個視窗下看到的波型數量愈來愈少。

III. 最後週期趨近於無限大的時候，無論視窗多寬，我們都只看得到原本的波型 (即無週期性)。

回憶一下第二節的結論，給定 $\displaystyle \ddot v(t) = \dfrac{a_0}2 + \sum_{n=1}^\infty \Big(a_n\cos(n\dfrac{2\pi}{T_0}t) + b_n\sin(n\dfrac{2\pi}{T_0}t)\Big)$，當 $T_0\to\infty$ 時原式其實可以化為： \displaystyle \begin{alignat*}{2} v(t) &= \lim_{T_0\to\infty}\dfrac{a_0}2 + \frac1{T_0}\cdot\sum_{n=1}^\infty T_0a_n\cos(n\dfrac{2\pi}{T_0}t) + T_0b_n\sin(n\dfrac{2\pi}{T_0}t) \\&= \lim_{T_0\to\infty} \bigg(\dfrac1{T_0}\int_{T_0} v(t)\ dt\bigg) + \frac1{T_0}\cdot\sum_{n=1}^\infty T_0a_n\cos(n\dfrac{2\pi}{T_0}t) + T_0b_n\sin(n\dfrac{2\pi}{T_0}t)\quad\quad\ //\ \dfrac1{T_0}\int_{T_0} v(t)\ dt = 0\\&= \lim_{T_0\to\infty}\frac1{T_0}\cdot\sum_{n=1}^\infty \bigg(2\int_{T_0} v(t)\cos(n\dfrac{2\pi}{T_0}t)\ dt\bigg)\cos(n\dfrac{2\pi}{T_0}t) + \bigg(2\int_{T_0} v(t)\sin(n\dfrac{2\pi}{T_0}t)\ dt\bigg)\sin(n\dfrac{2\pi}{T_0}t)\quad\quad\ //\ 抽換掉\ T_0a_n\ 和\ T_0b_n\\&= \lim_{f_0\to0} f_0\cdot\sum_{n=1}^\infty \bigg(2\int_{-\infty}^\infty v(t)\cos\Big(2\pi(nf_0)t\Big)\ dt\bigg)\cos\Big(2\pi(nf_0)t\Big) + \bigg(2\int_{-\infty}^\infty v(t)\sin\Big(2\pi(nf_0)t\Big)\ dt\bigg)\sin\Big(2\pi(nf_0)t\Big)\quad\quad\ //\ 1/T_0\ 取代成\ f_0 \\&= \lim_{f_0\to0}f_0\cdot\sum_{n=1}^\infty A(nf_0)\cos\Big(2\pi(nf_0)t\Big) + B(nf_0)\sin\Big(2\pi(nf_0)t\Big)\quad\quad\ //\ 以頻率為參數定義出新的函數\\&= \int_{0}^\infty A(f)\cos(2\pi ft) + B(f)\sin(2\pi ft)\ df\quad\quad\ //\ 將黎曼和轉為積分\end{alignat*} 至此，我們終於確立了非週期性訊號的傅立葉合成式！和 FS 較為明顯的差異相信讀者可以觀察到，便在於頻譜從離散形式的 $a_n$、$b_n$ 乘上週期 $T_0$之後變成連續形式的$A(f)$、$B(f)$了。

　　　　　　　　　　時限訊號的傅立葉積分 (Fourier Integral，簡稱 FI)

給定一個定義於整個實數域的非週期性時限訊號 $v(t)$，其傅立葉積分定義如下：

　　　　　　　　　　$\displaystyle \int_{0}^\infty A(f)\cos(2\pi ft) + B(f)\sin(2\pi ft)\ df$　　　　　　　　　　 其中$\displaystyle A(f) = 2\int_{-\infty}^\infty v(t)\cos(2\pi ft)\ dt$，而且$\displaystyle B(f) = 2\int_{-\infty}^\infty v(t)\sin(2\pi ft)\ dt$，這是對於所有的正實數 $f$ 而言 (不包含 0)。

# 推廣到非時限訊號

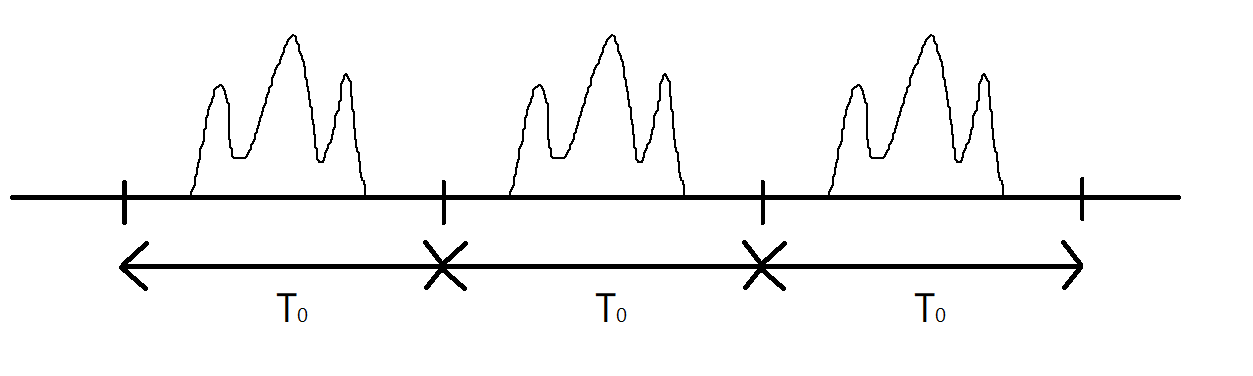
細心的讀者應該會發現，其實還有一種更通俗的情況還沒考慮到。我們剛剛的推導都是在時限的假設底下進行，在理論數學模型底下的所有訊號，應該存在非時限的訊號吧？如果不是時限訊號的話要怎麼辦呢？其實可以用分段的技巧，將整段長訊號切割成一小段一小段的時限訊號，重複時限訊號的表示式最後再行累加即可，依然會導到預期與時限訊號一樣的結論。概念圖如下：

I. 原本非時限訊號有無限長。

II. 最後可以拆成無數個時限訊號的疊加。

假如非時限訊號 $v(t)$可以拆解成無窮多個時限訊號的疊合 $\displaystyle \sum_{i=1}^\infty v_i(t)$，那麼： I. 從時域的疊加觀點來看 $\displaystyle v(t) = \sum_{i=1}^\infty v_i(t)$

　　　　　　　　　 　　　　$\displaystyle = \sum_{i=1}^\infty \bigg( \int_{0}^\infty A_i(f)\cos(2\pi ft) + B_i(f)\sin(2\pi ft)\ df\bigg)$

　　　　　　　　　　　　　 $\displaystyle = \int_{0}^\infty \bigg(\sum_{i=1}^\infty A_i(f)\bigg)\cos(2\pi ft) + \bigg(\sum_{i=1}^\infty B_i(f)\bigg)\sin(2\pi ft)\ df$

　　　　　　　　　　　　　 $\displaystyle = \int_{0}^\infty A(f)\cos(2\pi ft) + B(f)\sin(2\pi ft)\ df$

我們依然可以有類似時限訊號的結論 $\displaystyle v(t) = \int_{0}^\infty A(f)\cos(2\pi ft) + B(f)\sin(2\pi ft)\ df$。 另外，從推導也恰好得知 $\displaystyle A(f)=\sum_{i=1}^{\infty}A_i(f)$且 $\displaystyle B(f)=\sum_{i=1}^{\infty}B_i(f)$，意味著頻譜也必須隨之疊加。

II. 從頻域的疊加觀點來看 $\displaystyle A(f) = \sum_{i=1}^\infty A_i(f) = \sum_{i=1}^\infty \Bigg(2\int_{-\infty}^\infty v_i(t)\cos(2\pi ft)\ dt \Bigg)$ 　　　　　　　　　　　　　 　$\displaystyle = 2\int_{-\infty}^\infty \bigg( \sum_{i=1}^\infty v_i(t)\bigg)\cos(2\pi ft)\ dt = 2\int_{-\infty}^\infty v(t)\cos(2\pi ft)\ dt$，同理 $\displaystyle B(f) = 2\int_{-\infty}^\infty v(t)\sin(2\pi ft)\ dt$。我們依然可以有類似時限訊號的結論。

　　　　　　　　　　　　推廣 1 － 推廣傅立葉積分到非時限訊號

藍框框所敘述的傅立葉積分定義也可以適用到非時限訊號。