(*) 第一節 - 理論的起源

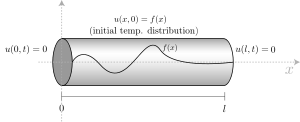
要介紹詳細的理論之前其實應該先解釋什麼是傅立葉級數，本節主要是簡述歷史的部分，覺得冗長的讀者大可直接略過沒有關係，並不影響理解後續定理的邏輯推演。其實自然界裡正常的時限訊號 ($u(t)=0$for $t\in\mathbb R\setminus[a,b]$ where $a\le b$) 能表為各種三角級數總和的這個想法並非憑空產生，而是由法國數學家 Joseph Fourier 在研究熱傳導問題時所提出來的。在 1822 年出版的關於熱傳導的重要數學著作《熱的解析理論》[1][2][3] 裡面，他探討了許多不同形狀 (矩形、環狀、球狀、柱狀、稜柱形) [4] 底下偏微分方程式的解，而這些的解出來就是現在眾所周知的「三角級數和」，具體的偏微分方程式問題根據筆者在網路花上大把工夫的 survey 之後發現，比較會特別提出來談的主要有兩個：一個是在 $t\ge0$、$0\le x\le\pi$ 範圍中$\displaystyle \frac{\partial u}{\partial t} = \frac{\partial^2 u}{\partial x^2}$附帶邊界條件之 $u(0,t) = u(\pi,t) = 0$ 的初始條件$u(x,0) = f(x)$ 必能表成正弦波們的總和 $\displaystyle \sum_{n=1}^\infty b_n\sin nx$ [5][6][7][8][9]；

另外一個是在 $x\ge0$、$|y|\le\dfrac\pi2$的範圍中$\displaystyle \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = 0$ 附帶邊界條件之 $u(x,\pm\dfrac\pi2)=0$ 所伴隨的另一個邊界條件 $u(0,y) = f(y)$ 必定能表成各種正餘弦波的總和 $\displaystyle \dfrac{a_0}2 + \sum_{n=1}^\infty a_n\cos ny + b_n\sin ny$ [4][10]。無論從什麼問題出發，他終究到達了「三角級數和」這個結論。

偉大的約瑟夫．傅立葉 (Jean Baptiste Joseph Fourier，1768 年 3 月 21 日 － 1830 年 5 月 16 日)

事實上傅立葉並不是第一位提出「三角級數和」這個想法的學者，在他之前就有許多的數學家例如 Daniel Bernoulli (1700－1782)、Leonard Euler (1707－1783)、Jean le Rond d'Alembert (1717－1783) 等人針對弦振動問題有了一番論戰而且有「三角級數和」之猜想 [4][5][7][11]，只是傅立葉因為求解熱傳導微分方程的動機而把這猜想又發展成更完整的理論，他最主要的貢獻在於為了處理無窮區域的熱傳導問題而推導出傅立葉積分 (第四節) [12][13]，且為了理論的合理性又重新解釋了積分的意義 [4][5]。至於傅立葉級數是否能收斂回原函數的充分條件至少要等到德國大數學家 Peter Gustav Lejeune-Dirichlet (1805－1859) 於 1829 年在 Crele 雜誌上所發表的關於傅立葉級數之最著名的文章〈關於三角級數的收斂性〉(Sur la convergence des séries trigonométriques qui servent à représenter une fonction arbitraire entre des limites données) [14][15] 才有個較為正式的論述 [4]。