第二節 - DFT 的運算性質

在本節我們要介紹三個關於 DFT 的有趣性質，它們分別是：

• 時頻域皆以 N 點為一週期 (Periodic in k and in n with fundamental period of N)

• 訊號補零使頻譜趨近於 DTFT (Zero padding in time domain)

• 循環摺積 (Circular convolution)

# 時頻域皆以 N 點為一週期 (Periodic in k and in n with fundamental period of N)

這其實在上一章已經推導過，時域取樣造成頻譜週期性、頻域取樣造成時域週期性。這邊再次點出造成此現象的關鍵恆等式。

(*) $e^{-j2\pi\frac kNn} = e^{-j2\pi\frac {(k+iN)}Nn}$ for all $i\in\mathbb Z$ implies $X[k] = X[k+iN]$.

(*) $e^{+j2\pi\frac kNn} = e^{+j2\pi\frac {(k+iN)}Nn}$ for all $i\in\mathbb Z$ implies $x[k] = x[k+iN]$.

# 訊號補零使頻譜趨近於 DTFT (Zero padding in time domain)

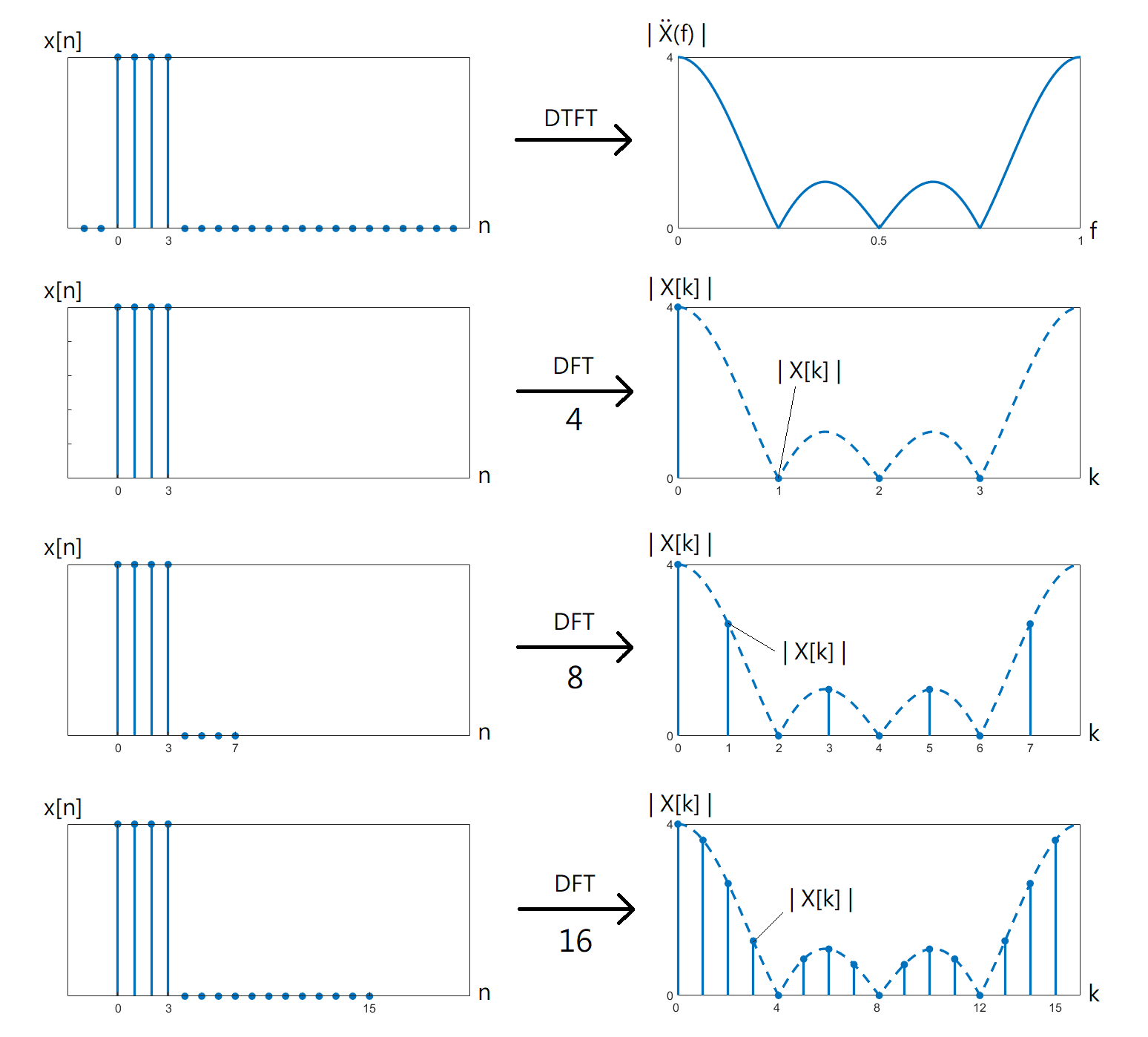
給定一段時限離散訊號，當它作 DFT 之前的補零點數愈多，其離散頻譜會愈接近該時限訊號的 DTFT (連續頻譜)，或者反過來說就是我們之前在第四章第五節得到的結論，對頻譜取樣確實會造成訊號週期性疊加。這邊先給出一張示意圖培養感覺：(如果覺得太小的話可以直接用滑鼠對圖片按一下，會自動放大)

這張圖片裡的第一組是單純的對時限訊號作 DTFT，而後三組則是觀察在原訊號補零的個數會對 DFT 造成什麼影響，的確是可以發現到點數愈多，DFT 就愈接近 DTFT (離散頻譜解析度愈高)，讀者也可以親自寫程式碼跑實驗來體會一下它背後的涵義，這也說明了為什麼第四節直接拿 DFT 來作訊號處理會很適合了。

關於數學證明的理解，我們必須回到第四章第五節 DTFT → DTFS 的推導，這邊直接設定 $T_s=f_s=1$：

\displaystyle \begin{alignat*}{2} \ddot X\Big(\frac kN\Big) &= \sum_{n=-\infty}^\infty x[n]\ e^{-j2\pi\frac kNn} \\&= \sum_{n=<N>}\sum_{i=-\infty}^\infty x[n+iN]\ e^{-j2\pi\frac kN(n+iN)} \\&= \sum_{n=<N>}\underline{\sum_{i=-\infty}^\infty x[n+iN]}\ e^{-j2\pi\frac kNn}=X[k]\quad\quad//\ \text{DFT }(這裡用這個) \\&= \dfrac1N\sum_{n=<N>}\underline{N\sum_{i=-\infty}^\infty x[n+iN]}\ e^{-j2\pi\frac kNn} = X_k\quad\quad//\ \text{DTFS }(不要用這個)\end{alignat*}

注意到這邊必須使用 DFT 的版本，從式子來看也的確和上圖相吻合！

# 循環摺積 (Circular convolution) [2]

這邊和一般「對兩個離散訊號之頻譜乘積作傅立葉反轉換會得到線性摺積」的結論有所不同，因為對 DFT 的視角來說訊號是有隱含週期性的，所以這邊是「循環」摺積的特性，證明如下。

\displaystyle \begin{alignat*}{2}y[n] &= \frac1N\sum_{k=0}^{N-1}Y[k]\ e^{j2\pi\frac kNn}\\&=\frac1N\sum_{k=0}^{N-1}\Big(H[k]\ X[k]\Big)\ e^{j2\pi\frac kNn}\\&=\frac1N\sum_{k=0}^{N-1}\Big(\sum_{m=0}^{N-1}h[m]\ e^{-j2\pi\frac kNm}\Big)\ X[k]\ e^{j2\pi\frac kNn}\\&=\sum_{m=0}^{N-1}h[m]\cdot\Big(\frac1N\sum_{k=0}^{N-1}X[k]\ e^{j2\pi\frac kN(n-m)}\Big)\\&=\sum_{m=0}^{N-1}h[m]\cdot x\Big[(n-m)\text{ mod }N\Big]\end{alignat*}

注意到輸入訊號 $x$ 的索引值能$\text{mod }N$的原因是$e^{j2\pi\frac kNn} = e^{j2\pi\frac kN(n+iN)}\text{ for all integers }i$，而這便是「循環」摺積的由來，簡單來說「線性」和「循環」最大的差別在於索引值如果超出原訊號範圍，前者會直接補零，後者則平移一個週期由範圍內的訊號遞補。